��֪�Ax2+y2=R2���t���ˈA��(n��i)һ�c(di��n)A��a��b����a��b��ͬ�r��0��ƽ�ֵ������ڵ�ֱ�����̞� ��
���𰸡�
���������}�����֪�R�c(di��n)�ǣ�ֱ���c�A�ཻ�����|(zh��)����ֱ����һ��ʽ���̣��ɴ���������֪���M��l�����ң��^A�c(di��n)�����c��(j��ng)�^�A�ģ�ԭ�c(di��n)�����c(di��n)A��ֱ����ֱ���ɴ��҂�Ҫ��ֱ���ķ��̣���������ֱ����б�ʣ�Ȼ������бʽ���̣�������Ĵ𰸣�
����⣺�ɴ���������֪���M��l�������^A�c(di��n)��
���c��(j��ng)�^�A�ģ�ԭ�c(di��n)�����c(di��n)A��ֱ����ֱ
��ֱ����б��k=
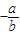
����ֱ���^�c(di��n)A��a��b��
�tֱ���ķ��̞飺
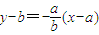
��ax+by-a
2-b
2=0
���xAx+by-a
2-b
2=0
�c(di��n)�u������ֱ�����̕r����(y��ng)���x���m��(d��ng)?sh��)�ֱ�����̵���ʽ����ע����N��ʽ���m�×l������б��ʽ���c(di��n)бʽ�r��ֱ����б�ʱ�횴��ڣ������c(di��n)ʽ���ܱ�ʾ�c����(bi��o)�S��ֱ��ֱ�����ؾ�ʽ���ܱ�ʾ�c����(bi��o)�S��ֱ��(j��ng)�^ԭ�c(di��n)��ֱ�������ڽ��}�r�������ýؾ�ʽ����(y��ng)ע����ӑՓ���Д�ؾ��Ƿ���㣻�������c(di��n)бʽ����(y��ng)�ȿ��]б�ʲ����ڵ���r��

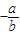
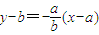


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
С�W(xu��)��10��犑�(y��ng)���}ϵ�д�