日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情

已知中，三條邊所對的角分別為、、，且.

（1）求角的大小；

（2）若，求的最大值.

 

【答案】

（1）；（2）.

【解析】

試題分析：（1）在已知條件中，利用邊角互化將條件轉化為，于此得到的值，從而求出角的大小；（2）先利用二倍角的降冪公式與輔助角公式將函數的解析式化簡為，在（1）的條件下，得到的取值范圍是，問題轉化為求函數在區間上取最大值，只需先求的取值范圍，結合正弦曲線確定函數的最大值.

試題解析：（1）由正弦定理，，由

；

（2），所以

由（1），.

考點：1.邊化角；2.二倍角公式；3.輔助角公式；4.三角函數的最值

 

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

已知在△ABC中，三條邊a、b、c所對的角分別為A、B、C，向量
m
=（sinA，cosA），
n
=（cosB，sinB），且滿足
m
•
n
=sin2C．
（1）求角C的大小；
（2）若sinA、sinC、sinB成等差數列，且
CA
•(
AB
-
AC
)=18，求c的值．

查看答案和解析>>

科目：高中數學 來源： 題型：

已知△ABC中，三條邊a、b、c所對的角分別為A、B、C，且bsinA=
3
acosB．
（1）求角B的大小；
（2）若f(x)=
3
sinxcosx+cos2x，求f（A）的最大值．

查看答案和解析>>

科目：高中數學 來源：2010-2011學年天津市高三上學期期中考試數學理卷 題型：解答題

（12分）

已知在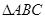中，三條邊所對的角分別為，向量，且滿足。

（1）求角的大小；

（2）若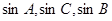成等比數列，且，求的值。

 

查看答案和解析>>

科目：高中數學 來源：《第2章 平面向量》2010年單元測試卷（7）（解析版） 題型：解答題

已知在△ABC中，三條邊a、b、c所對的角分別為A、B、C，向量=（sinA，cosA），=（cosB，sinB），且滿足．
（1）求角C的大小；
（2）若sinA、sinC、sinB成等差數列，且=18，求c的值．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 国产黄av | 91资源总站 | a性视频 | 日韩avav | 欧美二区三区 | 免费看黄网址 | 久久精品免费观看 | 欧美欧美欧美 | 日韩精品在线一区二区 | 黄站在线观看 | 久久久.com | 午夜视频福利 | 久久久综合亚洲91久久98 | 欧美三级电影在线观看 | 午夜免费av | 美女日日日 | 国产日韩欧美在线 | 欧州一区二区三区 | 欧美日韩在线免费 | 免费av一区二区三区 | 黄色av网站在线观看 | 久草热久草在线 | 欧美性猛交一区二区三区精品 | 狠狠干狠狠干 | 污网址在线免费观看 | 久久不卡 | h视频网站在线 | 天天干天天操天天舔 | 久久爱综合网 | 日日人人 | 亚洲精品国产综合区久久久久久久 | 国产成人精品午夜视频免费 | 一区二区在线视频 | 亚洲视频在线一区二区三区 | 91视频电影| 国产精品99 | 日韩欧美中文在线观看 | 日本一本视频 | 黄色网址免费在线观看 | 国产精品视频福利 | 成人黄色免费观看 |