由方程2x|x|-y=1所確定的x,y的函數關系記為y=f(x).給出如下結論:
①f(x)是R上的單調遞增函數;
②對于任意x∈R,f(x)+f(-x)=-2恒成立;
③存在x0∈(-1,0),使得過點A(1,f(1)),B(x0,f(x0))的直線與曲線f(x)恰有兩個公共點.
其中正確的結論為________(寫出所有正確結論的序號).
①②③
分析:由方程2x|x|-y=1所確定的x,y的函數關系記為y=f(x),f(x)=2x|x|-1=
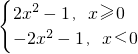
,分別畫出當x≥0和x<0的函數圖象,它們分別是拋物線的一部分.如圖所示.結合觀察圖象可得答案.
解答:
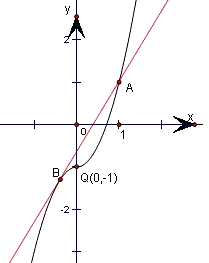
解:由方程2x|x|-y=1所確定的x,y的函數關系記為y=f(x),
則f(x)=2x|x|-1=
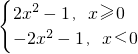
,
分別畫出當x≥0和x<0的函數圖象,它們分別是拋物線的一部分.如圖所示.
觀察圖象可知:
①f(x)是R上的單調遞增函數; 正確;
②圖象關于點Q(0,-1)對稱,故對于任意x∈R,f(x)+f(-x)=-2恒成立;正確;
③當點B是過點A(1,f(1)),B(x
0,f(x
0))的直線與曲線相切時的切點時,過點A(1,f(1)),B(x
0,f(x
0))的直線與曲線f(x)恰有兩個公共點,故存在x
0∈(-1,0),使得過點A(1,f(1)),B(x
0,f(x
0))的直線與曲線f(x)恰有兩個公共點;正確.
故其中正確的結論為 ①②③.
故答案為:①②③.
點評:本小題主要考查分段函數、函數單調性的應用、函數對稱性的應用、帶絕對值的函數等基礎知識,考查運算求解能力,考查數形結合思想、化歸與轉化思想.屬于基礎題.

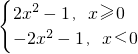 ,分別畫出當x≥0和x<0的函數圖象,它們分別是拋物線的一部分.如圖所示.結合觀察圖象可得答案.
,分別畫出當x≥0和x<0的函數圖象,它們分別是拋物線的一部分.如圖所示.結合觀察圖象可得答案.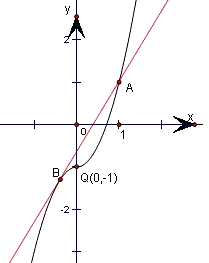 解:由方程2x|x|-y=1所確定的x,y的函數關系記為y=f(x),
解:由方程2x|x|-y=1所確定的x,y的函數關系記為y=f(x),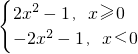 ,
,
