
【題目】如圖,在四棱錐E﹣ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,且AB=4,BC=CD=ED=EA=2. 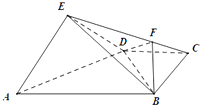
(1)求二面角E﹣AB﹣D的正切值;
(2)在線段CE上是否存在一點F,使得平面EDC⊥平面BDF?若存在,求 ![]() 的值,若不存在請說明理由.
的值,若不存在請說明理由.
【答案】
(1)解:取AD的中點H,則EH⊥AD,
又平面EAD⊥平面ABCD,
∴EH⊥平面ABCD,
過H作HN⊥AB于N,由EN⊥AB,
∴∠ENH為二面角E﹣AB﹣D的平面角,
又∵BC⊥AB,AB∥CD,AB=2CD=4,
∴AD=2 ![]() ,AH=
,AH= ![]() ,AE=2,∴EH=
,AE=2,∴EH= ![]() ,
,
又HN=1,∴tan ![]() ,
,
∴二面角E﹣AB﹣D的正切值為 ![]()
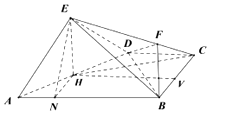
(2)解:存在點F滿足條件.
取AB的中點M,由DM= ![]() AB,故DB⊥AD,
AB,故DB⊥AD,
又平面EAD⊥平面ABCD,
∴BD⊥平面EAD,∴BD⊥ED,
要使平面EDC⊥平面BDF,
在等腰△DEC,DE=DC=2,EC= ![]() =2
=2 ![]() ,
,
∴∠DEC=30°,∴EF= ![]() .
.
∴ ![]() =
= ![]() .
.
【解析】(1)取AD的中點H,則EH⊥AD,EH⊥平面ABCD,過H作HN⊥AB于N,由EN⊥AB,得∠ENH為二面角E﹣AB﹣D的平面角,由此能求出二面角E﹣AB﹣D的正切值.(2)取AB的中點M,推導出DB⊥AD,BD⊥ED,由此能求出 ![]() 的值.
的值.
【考點精析】通過靈活運用平面與平面垂直的性質,掌握兩個平面垂直,則一個平面內垂直于交線的直線與另一個平面垂直即可以解答此題.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣a2x2+ax(a∈R).
(1)當a=1時,求函數f(x)最大值;
(2)若函數f(x)在區間(1,+∞)上是減函數,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用m,n表示兩條不同的直線,α,β表示兩個不同的平面,給出下列命題: ①若m⊥n,m⊥α,則n∥α;
②若m∥α,α⊥β則m⊥β;
③若m⊥β,α⊥β,則m∥α;
④若m⊥n,m⊥α,n⊥β,則α⊥β,
其中,正確命題是( )
A.①②
B.②③
C.③④
D.④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐![]() 中,底面
中,底面![]() 是邊長為 2 的正三角形,頂點
是邊長為 2 的正三角形,頂點 ![]() 在底面
在底面![]() 上的射影為
上的射影為![]() 的中心,若
的中心,若![]() 為
為![]() 的中點,且直線
的中點,且直線![]() 與底面
與底面![]() 所成角的正切值為
所成角的正切值為![]() ,則三棱錐
,則三棱錐![]() 外接球的表面積為( )
外接球的表面積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x3+(1﹣a)x2﹣a(a+2)x+b(a,b∈R).
(1)若函數f(x)的圖象過原點,且在原點處的切線斜率為﹣3,求a,b的值;
(2)若曲線y=f(x)存在兩條垂直于y軸的切線,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校對高三學生一次模擬考試的數學成績進行分析,隨機抽取了部分學生的成績,得到如圖所示的成績頻率分布直方圖.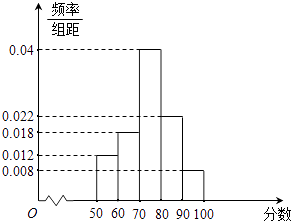
(1)根據頻率分布直方圖估計這次考試全校學生數學成績的眾數、中位數和平均值;
(2)若成績不低于80分為優秀成績,視頻率為概率,從全校學生中有放回的任選3名學生,用變量ξ表示3名學生中獲得優秀成績的人數,求變量ξ的分布列及數學期望E(ξ).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某景點擬建一個扇環形狀的花壇(如圖所示),按設計要求扇環的周長為36米,其中大圓弧所在圓的半徑為14米,設小圓弧所在圓的半徑為![]() 米,圓心角為
米,圓心角為![]() (弧度).
(弧度).
⑴ 求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
⑵ 已知對花壇的邊緣(實線部分)進行裝飾時,直線部分的裝飾費用為4元/米,弧線部分的裝飾費用為16元/米,設花壇的面積與裝飾總費用之比為![]() ,求
,求![]() 關于
關于![]() 的函數關系式,并求出
的函數關系式,并求出![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在封閉的直三棱柱ABC﹣A1B1C1內有一個體積為V的球,若AB⊥BC,AB=6,BC=8,AA1=5,則V的最大值是( )
A.4π
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com