【答案】
分析:(1)先對函數f(x)進行求導,令導函數大于0可求函數的增區間,令導函數小于0可求函數的減區間.
(2)在區間[0,2]上恒有f(x)≥-

,等價于x∈[0,2]時f(x)
min≥-

,借助(1)問函數的單調性可求其最小值.
解答:解:(1)f'(x)=x
2-a
2=(x-a)(x+a)(a>0)
f'(x)>0⇒x>a或x<-a,f'(x)<0⇒-a<x<a…(4分)
∴f(x)在(-∞,-a)和(a,+∞)上都單調遞增,在[-a,a]上單調遞減;…(6分)
(2)x=-a為函數y=f(x)的極大值點,x=a為函數y=f(x)的極小值點,…(8分)
①當0<a<2時,函數y=f(x)在[0,2]上的最小值為f(a)=-

a
3+2a,
∴-

a
3+2a
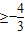
,即(a+1)
2(a-2)≤0,∴a≤2,又0<a<2
∴0<a<2…(11分)
②當a≥2時,函數y=f(x)在[0,2]上的最小值為f(2)=
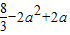
,
∴
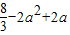
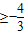
,∴-1≤a≤2
又a≥2,∴a=2,…(14分)
綜上,0<a≤2.…(15分).
點評:本題考查的知識點是利用導數求閉區間上函數的最值,利用導數研究函數的單調性,熟練掌握導函數法求函數單調區間和最值的方法和步驟是解答的關鍵.

 x3-a2x+2a,(a>0)
x3-a2x+2a,(a>0) ,求a的取值范圍.
,求a的取值范圍. ,等價于x∈[0,2]時f(x)min≥-
,等價于x∈[0,2]時f(x)min≥- ,借助(1)問函數的單調性可求其最小值.
,借助(1)問函數的單調性可求其最小值. a3+2a,
a3+2a, a3+2a
a3+2a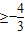 ,即(a+1)2(a-2)≤0,∴a≤2,又0<a<2
,即(a+1)2(a-2)≤0,∴a≤2,又0<a<2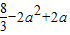 ,
,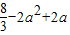
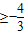 ,∴-1≤a≤2
,∴-1≤a≤2

 已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<