
【題目】已知 ![]() ≤a≤1,若函數f(x)=ax2﹣2x+1在區間[1,3]上的最大值為M(a),最小值為N(a),令g(a)=M(a)﹣N(a).
≤a≤1,若函數f(x)=ax2﹣2x+1在區間[1,3]上的最大值為M(a),最小值為N(a),令g(a)=M(a)﹣N(a).
(1)求g(a)的函數表達式;
(2)判斷函數g(a)在區間[ ![]() ,1]上的單調性,并求出g(a)的最小值.
,1]上的單調性,并求出g(a)的最小值.
【答案】
(1)解:f(x)=ax2﹣2x+1的對稱軸為x= ![]() ,
,
∵ ![]() ≤a≤1,∴1≤
≤a≤1,∴1≤ ![]() ≤3,
≤3,
∴f(x)在[1,3]上的最小值f(x)min=N(a)=f( ![]() )=1﹣
)=1﹣ ![]() .
.
∵f(x)=ax2﹣2x+1在區間[1,3]上的最大值為M(a),最小值為N(a),
∴①當1≤ ![]() ≤2,即
≤2,即 ![]() ≤a≤1時,
≤a≤1時,
M(a)=f(3)=9a﹣5,N(a)=f( ![]() )=1﹣
)=1﹣ ![]() .
.
g(a)=M(a)﹣N(a)=9a+ ![]() ﹣6.
﹣6.
②當2< ![]() ≤3時.即
≤3時.即 ![]() ≤a<
≤a< ![]() 時,
時,
M(a)=f(1)=a﹣1,N(a)=f( ![]() )=1﹣
)=1﹣ ![]() .
.
g(a)=M(a)﹣N(a)=a+ ![]() ﹣2.
﹣2.
∴g(a)= 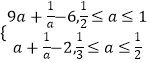
(2)解:由(1)可知當 ![]() ≤a≤1時,g(a)=M(a)﹣N(a)=9a+
≤a≤1時,g(a)=M(a)﹣N(a)=9a+ ![]() ﹣6≥0,當且僅當a=
﹣6≥0,當且僅當a= ![]() 時取等號,所以它在[
時取等號,所以它在[ ![]() ,1]上單調遞增;
,1]上單調遞增;
當 ![]() ≤a<
≤a< ![]() 時,g(a)=M(a)﹣N(a)=a+
時,g(a)=M(a)﹣N(a)=a+ ![]() ﹣2≥0,當且僅當a=1時取等號,所以g(a)在[
﹣2≥0,當且僅當a=1時取等號,所以g(a)在[ ![]() ]單調遞減.
]單調遞減.
∴g(a)的最小值為g( ![]() )=9×
)=9× ![]()
【解析】(1)明確f(x)=ax2﹣2x+1的對稱軸為x= ![]() ,由
,由 ![]() ≤a≤1,知1≤
≤a≤1,知1≤ ![]() ≤3,可知f(x)在[1,3]上單調遞減,N(a)=f(
≤3,可知f(x)在[1,3]上單調遞減,N(a)=f( ![]() )=1﹣
)=1﹣ ![]() .由a的符號進行分類討論,能求出g(a)的解析式;(2)根據(1)的解答求g(a)的最值.
.由a的符號進行分類討論,能求出g(a)的解析式;(2)根據(1)的解答求g(a)的最值.
【考點精析】解答此題的關鍵在于理解函數單調性的判斷方法的相關知識,掌握單調性的判定法:①設x1,x2是所研究區間內任兩個自變量,且x1<x2;②判定f(x1)與f(x2)的大小;③作差比較或作商比較,以及對二次函數在閉區間上的最值的理解,了解當![]() 時,當
時,當![]() 時,
時,![]() ;當
;當![]() 時在
時在![]() 上遞減,當
上遞減,當![]() 時,
時,![]() .
.


 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:高中數學 來源: 題型:
【題目】選修![]() :坐標系與參數方程選講.
:坐標系與參數方程選講.
在平面直角坐標系![]() 中,曲線
中,曲線![]() (
(![]() 為參數,實數
為參數,實數![]() ),曲線
),曲線![]()
![]() (
(![]() 為參數,實數
為參數,實數![]() ). 在以
). 在以![]() 為極點,
為極點, ![]() 軸的正半軸為極軸的極坐標系中,射線
軸的正半軸為極軸的極坐標系中,射線![]() 與
與![]() 交于
交于![]() 兩點,與
兩點,與![]() 交于
交于![]() 兩點. 當
兩點. 當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() .
.
(1)求![]() 的值; (2)求
的值; (2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,過橢圓
中,過橢圓![]() 右焦點的直線
右焦點的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,
兩點, ![]() 為
為![]() 的中點,且直線
的中點,且直線![]() 的斜率為
的斜率為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設另一直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,原點
兩點,原點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,已知點
中,已知點![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為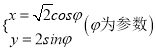 .以原點為極點,
.以原點為極點, ![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為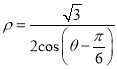 .
.
(Ⅰ)判斷點![]() 與直線
與直線![]() 的位置關系并說明理由;
的位置關系并說明理由;
(Ⅱ)設直線![]() 與曲線
與曲線![]() 的兩個交點分別為
的兩個交點分別為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知多面體![]() 如圖所示.其中
如圖所示.其中![]() 為矩形,
為矩形, ![]() 為等腰直角三角形,
為等腰直角三角形, ![]() ,四邊形
,四邊形![]() 為梯形,且
為梯形,且![]() ,
, ![]() ,
, ![]() .
.

(1)若![]() 為線段
為線段![]() 的中點,求證:
的中點,求證: ![]() 平面
平面![]() .
.
(2)線段![]() 上是否存在一點
上是否存在一點![]() ,使得直線
,使得直線![]() 與平面
與平面![]() 所成角的余弦值等于
所成角的余弦值等于![]() ?若存在,請指出點
?若存在,請指出點![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017唐山模擬】如圖,ABCDA1B1C1D1為正方體,連接BD,AC1,B1D1, CD1,B1C,現有以下幾個結論:①BD∥平面CB1D1;②AC1⊥平面CB1D1;③AC1與底面ABCD所成角的正切值是;④CB1與BD為異面直線,其中所有正確結論的序號為________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)=kax﹣a﹣x(a>0且a≠1)在(﹣∞,+∞)上既是奇函數又是增函數,則函數g(x)=loga(x+k)的圖像是( )
A.
B.
C.
D.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將直角三角形![]() 沿斜邊上的高
沿斜邊上的高![]() 折成
折成![]() 的二面角,已知直角邊
的二面角,已知直角邊![]() ,
, ![]() ,那么下面說法正確的是( )
,那么下面說法正確的是( )
A. 平面![]() 平面
平面![]()
B. 四面體![]() 的體積是
的體積是![]()
C. 二面角![]() 的正切值是
的正切值是![]()
D. ![]() 與平面
與平面![]() 所成角的正弦值是
所成角的正弦值是![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com