解:(I)由題意可知f′(x)=x
2-2(1+a)x+4a=(x-2)(x-2a)
(1)當a=1時,此時f′(x)=(x-2)
2≥0,所以原函數f(x)在R上為增函數
(2)當a>1時,此時由f′(x)>0可得x>2a或x<2
所以原函數f(x)在(-∞,2)和(2a,+∞)上為增函數,在(2,2a)上為減函數
綜合可知當a=1時原函數f(x)在R上為增函數,當a>1時原函數f(x)在(-∞,2)和(2a,+∞)上為增函數,在(2,2a)上為減函數
(II)存在.由題意可知只要f(x)在區間(0,+∞)上的最小值大于0即可.
(1)當a=1時,函數f(x)在R上為增函數,所以只需f(0)>0即可,顯然符合
(2)當a>1時因為函數f(x)在[0,2)和(2a,+∞)上為增函數,在(2,2a)上為減函數
所以此時只需
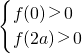
代入解得0<a<6
所以1<a<6
綜合(1)(2)可知1≤a<6
分析:(I)先求函數f(x)的導函數f′(x),再解不等式f′(x)>0和f′(x)<0即可得函數的單調區間,本題需討論a與1的關系;(II)先將問題轉化為求函數f(x)在[0,+∞)上的最小值大于零問題,再利用(I)中結論列不等式求a的范圍即可
點評:本題考查了導數在函數單調性中的應用,導數在求函數最值中的應用,不等式恒成立問題的解法,分類討論的思想方法

 x3-(1+a)x2+4ax+24a,其中常數a≥1
x3-(1+a)x2+4ax+24a,其中常數a≥1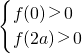 代入解得0<a<6
代入解得0<a<6
