
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根據共線向量基本定理及向量垂直的充要條件即可判斷出①②都為假命題,而根據基底的定義即可判斷出③命題正確,而根據向量數乘的幾何意義即可判斷命題④為假命題,這樣即可得出正確選項.
解答 解:①根據共線向量基本定理,$\overrightarrow{a}∥\overrightarrow{b}$的充要條件是存在實數λ,使得$\overrightarrow{b}=λ\overrightarrow{a}$,其中$\overrightarrow{a}≠\overrightarrow{0}$;
∵本命題沒限制$\overrightarrow{a}≠\overrightarrow{0}$;
∴本命題為假命題;
②若$\overrightarrow{a}•\overrightarrow{b}=0$,則$\overrightarrow{a}⊥\overrightarrow{b}$,其中$\overrightarrow{a},\overrightarrow{b}$可以都為非零向量;
∴該命題為假命題;
③若$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$不能構成空間的一個基底,則$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$共面;
∴O,A,B,C四點共面;
∴該命題正確;
④$\overrightarrow{a},\overrightarrow{c}$不共線,且$\overrightarrow{a}•\overrightarrow{b}≠0$時,$(\overrightarrow{a}•\overrightarrow{b})\overrightarrow{c}≠\overrightarrow{a}(\overrightarrow{b}•\overrightarrow{c})$;
∴該命題為假命題;
∴正確命題個數為1.
故選A.
點評 考查共線向量基本定理,向量垂直的充要條件,以及空間基底的定義,共面向量的定義,向量數乘的幾何意義.


科目:高中數學 來源: 題型:選擇題
| A. | 平行的兩條直線的斜率一定相等 | B. | 平行的兩條直線的傾斜角一定相等 | ||
| C. | 垂直的兩直線的斜率之積為-1 | D. | 斜率相等的兩條直線一定平行 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
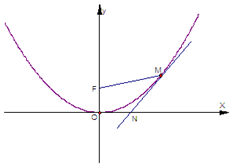 如圖,拋物線x2=4y在點$M(t,\;\frac{1}{4}{t^2})\;(t>0)$處的切線與x軸相交于點N,O、F分別為該拋物線的頂點、焦點.
如圖,拋物線x2=4y在點$M(t,\;\frac{1}{4}{t^2})\;(t>0)$處的切線與x軸相交于點N,O、F分別為該拋物線的頂點、焦點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com