
【題目】某中學為研究學生的身體素質與體育鍛煉時間的關系,對該校200名高三學生平均每天體育鍛煉時間進行調查,如表:(平均每天鍛煉的時間單位:分鐘)
平均每天鍛煉的時間/分鐘 |
|
|
|
|
|
|
總人數 | 20 | 36 | 44 | 50 | 40 | 10 |
將學生日均體育鍛煉時間在![]() 的學生評價為“鍛煉達標”.
的學生評價為“鍛煉達標”.
(1)請根據上述表格中的統計數據填寫下面![]() 列聯表;
列聯表;
鍛煉不達標 | 鍛煉達標 | 合計 | |
男 | |||
女 | 20 | 110 | |
合計 |
并通過計算判斷,是否能在犯錯誤的概率不超過0.025的前提下認為“鍛煉達標”與性別有關?
(2)在“鍛煉達標”的學生中,按男女用分層抽樣方法抽出5人,進行體育鍛煉體會交流,從參加體會交流的5人中,隨機選出2人作重點發言,求恰好選出一名男生的概率.
參考公式: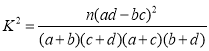 ,其中
,其中![]()
臨界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)![]() 列聯表答案見解析,在犯錯誤的概率不超過0.01的前提下不能判斷“課外體育達標”與性別有關;(2)
列聯表答案見解析,在犯錯誤的概率不超過0.01的前提下不能判斷“課外體育達標”與性別有關;(2)![]()
【解析】
(1)計算出觀測值![]() ,結合臨界值表可得結論;
,結合臨界值表可得結論;
(2)在“鍛煉達標”的學生有50人中,男女生人數比為![]() ,故用分層抽樣方法抽取5人,有3人是男生,記為a,b,c,有2人是女生,記為d,e,用列舉法以及古典概型概率公式可得結果.
,故用分層抽樣方法抽取5人,有3人是男生,記為a,b,c,有2人是女生,記為d,e,用列舉法以及古典概型概率公式可得結果.
(1)列出列聯表,
課外體育不達標 | 課外體育達標 | 合計 | |
男 | 60 | 30 | 90 |
女 | 90 | 20 | 110 |
合計 | 150 | 50 | 200 |
![]()
所以在犯錯誤的概率不超過0.01的前提下不能判斷“課外體育達標”與性別有關;
(2)“鍛煉打標”的學生有50人,男女生人數比為![]() ,故用分層抽樣
,故用分層抽樣
方法抽取5人,有3人是男生,記為a,b,c,有2人是女生,記為d,e,
則從這5人中選出2人,選法有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,共10種,
,共10種,
設事件A表示 “作重點發言的2人中,恰好有1名男生”,
則事件A包含的基本事件有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共6個,
共6個,
![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
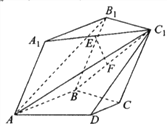
【題目】在如圖所示的多面體中,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 為邊長為2的菱形,
為邊長為2的菱形, ![]() 為直角梯形,四邊形
為直角梯形,四邊形![]() 為平行四邊形,且
為平行四邊形,且![]() ,
, ![]() ,
, ![]() .
.
(1)若![]() ,
, ![]() 分別為
分別為![]() ,
, ![]() 的中點,求證:
的中點,求證: ![]() 平面
平面![]() ;
;
(2)若![]() ,
, ![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區有小學21所,中學14所,大學7所,現采用分層抽樣的方法從這些學校中抽取6所學校對學生進行視力調查,若從抽取的6所學校中隨機抽取2所學校做進一步數據分析.
(1)求應從小學、中學、大學中分別抽取的學校數目;
(2)求抽取的6所學校中的2所學校均為小學的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點![]() 是拋物線
是拋物線![]() 的焦點,
的焦點,![]() 、
、![]() 是
是![]() 上兩點.若
上兩點.若![]() ,且線段
,且線段![]() 的中點到
的中點到![]() 軸的距離等于
軸的距離等于![]() .
.
(1)求![]() 的值;
的值;
(2)設直線![]() 與
與![]() 交于
交于![]() 、
、![]() 兩點且在
兩點且在![]() 軸的截距為負,過
軸的截距為負,過![]() 作
作![]() 的垂線,垂足為
的垂線,垂足為![]() ,若
,若![]() .
.
(i)證明:直線![]() 恒過定點,并求出該定點的坐標;
恒過定點,并求出該定點的坐標;
(ii)求點![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為實現國民經濟新“三步走”的發展戰略目標,國家加大了扶貧攻堅的力度,某地區在2015年以前的年均脫貧率(脫貧的戶數占當年貧困戶總數的比)為70%,2015年開始全面實施“精準扶貧”政策后,扶貧效果明顯提高,其中2019年度實施的扶貧項目,各項目參加戶數占比(參加戶數占2019年貧困總戶數的比)及該項目的脫貧率見下表:
實施項目 | 種植業 | 養殖業 | 工廠就業 |
參加占戶比 | 45% | 45% | 10% |
脫貧率 | 96% | 96% | 90% |
那么2019年的年脫貧率是實施“精準扶貧”政策前的年均脫貧率的( )倍.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓:![]() (a>b>0)過點E(
(a>b>0)過點E(![]() ,1),其左、右頂點分別為A,B,左、右焦點為F1,F2,其中F1(
,1),其左、右頂點分別為A,B,左、右焦點為F1,F2,其中F1(![]() ,0).
,0).
(1)求橢圓C的方程:
(2)設M(x0,y0)為橢圓C上異于A,B兩點的任意一點,MN⊥AB于點N,直線l:x0x+2y0y﹣4=0,設過點A與x軸垂直的直線與直線l交于點P,證明:直線BP經過線段MN的中點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com