
【題目】已知曲線![]() ,為直線
,為直線![]() 上的動點,過
上的動點,過![]() 作
作![]() 的兩條切線,切點分別為
的兩條切線,切點分別為![]() .
.
(1)證明:直線![]() 過定點:
過定點:
(2)若以![]() 為圓心的圓與直線
為圓心的圓與直線![]() 相切,且切點為線段
相切,且切點為線段![]() 的中點,求該圓的方程.
的中點,求該圓的方程.
【答案】(1)見詳解;(2) ![]() 或
或![]() .
.
【解析】
(1)可設![]() ,
,![]() ,
,![]() 然后求出A,B兩點處的切線方程,比如
然后求出A,B兩點處的切線方程,比如![]() :
:![]() ,又因為
,又因為![]() 也有類似的形式,從而求出帶參數直線
也有類似的形式,從而求出帶參數直線![]() 方程,最后求出它所過的定點.
方程,最后求出它所過的定點.
(2)由(1)得帶參數的直線![]() 方程和拋物線方程聯立,再通過
方程和拋物線方程聯立,再通過![]() 為線段
為線段![]() 的中點,
的中點,![]() 得出
得出![]() 的值,從而求出
的值,從而求出![]() 坐標和
坐標和![]() 的值,最后求出圓的方程.
的值,最后求出圓的方程.
(1)證明:設![]() ,
,![]() ,則
,則![]() 。又因為
。又因為![]() ,所以
,所以![]() .則切線DA的斜率為
.則切線DA的斜率為![]() ,故
,故![]() ,整理得
,整理得![]() .設
.設![]() ,同理得
,同理得![]() .
.![]() ,
,![]() 都滿足直線方程
都滿足直線方程![]() .于是直線
.于是直線![]() 過點
過點![]() ,而兩個不同的點確定一條直線,所以直線
,而兩個不同的點確定一條直線,所以直線![]() 方程為
方程為![]() .即
.即![]() ,當
,當![]() 時等式恒成立。所以直線
時等式恒成立。所以直線![]() 恒過定點
恒過定點![]() .
.
(2)由(1)得直線![]() 方程為
方程為![]() ,和拋物線方程聯立得:
,和拋物線方程聯立得:
 化簡得
化簡得![]() .于是
.于是![]() ,
,![]() 設
設![]() 為線段
為線段![]() 的中點,則
的中點,則![]()
由于![]() ,而
,而![]() ,
,![]() 與向量
與向量![]() 平行,所以
平行,所以![]() ,
,
解得![]() 或
或![]() .
.
當![]() 時,
時,![]() ,
,![]() 所求圓的方程為
所求圓的方程為![]() ;
;
當![]() 時,
時,![]() 或
或![]() ,
,![]() 所求圓的方程為
所求圓的方程為![]() .
.
所以圓的方程為![]() 或
或![]() .
.


 智趣寒假作業云南科技出版社系列答案
智趣寒假作業云南科技出版社系列答案科目:高中數學 來源: 題型:
【題目】2019年,我國施行個人所得稅專項附加扣除辦法,涉及子女教育、繼續教育、大病醫療、住房貸款利息或者住房租金、贍養老人等六項專項附加扣除.某單位老、中、青員工分別有![]() 人,現采用分層抽樣的方法,從該單位上述員工中抽取
人,現采用分層抽樣的方法,從該單位上述員工中抽取![]() 人調查專項附加扣除的享受情況.
人調查專項附加扣除的享受情況.
(Ⅰ)應從老、中、青員工中分別抽取多少人?
(Ⅱ)抽取的25人中,享受至少兩項專項附加扣除的員工有6人,分別記為![]() .享受情況如右表,其中“
.享受情況如右表,其中“![]() ”表示享受,“×”表示不享受.現從這6人中隨機抽取2人接受采訪.
”表示享受,“×”表示不享受.現從這6人中隨機抽取2人接受采訪.
員工 項目 | A | B | C | D | E | F |
子女教育 | ○ | ○ | × | ○ | × | ○ |
繼續教育 | × | × | ○ | × | ○ | ○ |
大病醫療 | × | × | × | ○ | × | × |
住房貸款利息 | ○ | ○ | × | × | ○ | ○ |
住房租金 | × | × | ○ | × | × | × |
贍養老人 | ○ | ○ | × | × | × | ○ |
(i)試用所給字母列舉出所有可能的抽取結果;
(ii)設![]() 為事件“抽取的2人享受的專項附加扣除至少有一項相同”,求事件
為事件“抽取的2人享受的專項附加扣除至少有一項相同”,求事件![]() 發生的概率.
發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() 的離心率是
的離心率是![]() ,一個頂點是
,一個頂點是![]() .
.

(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設![]() ,
,![]() 是橢圓
是橢圓![]() 上異于點
上異于點![]() 的任意兩點,且
的任意兩點,且![]() .試問:直線
.試問:直線![]() 是否恒過一定點?若是,求出該定點的坐標;若不是,說明理由.
是否恒過一定點?若是,求出該定點的坐標;若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,點P到兩點(0,![]() ),(0,
),(0,![]() ),的距離之和等于4,設點P的軌跡為C.
),的距離之和等于4,設點P的軌跡為C.
(1)求C的方程.
(2)設直線![]() 與C交于A,B兩點,求弦長|AB|,并判斷OA與OB是否垂直,若垂直,請說明理由.
與C交于A,B兩點,求弦長|AB|,并判斷OA與OB是否垂直,若垂直,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知點![]() 為拋物線
為拋物線![]() ,點
,點![]() 為焦點,過點
為焦點,過點![]() 的直線交拋物線于
的直線交拋物線于![]() 兩點,點
兩點,點![]() 在拋物線上,使得
在拋物線上,使得![]() 的重心
的重心![]() 在
在![]() 軸上,直線
軸上,直線![]() 交
交![]() 軸于點
軸于點![]() ,且
,且![]() 在點
在點![]() 右側.記
右側.記![]() 的面積為
的面積為![]() .
.
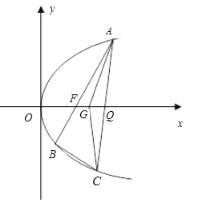
(1)求![]() 的值及拋物線的標準方程;
的值及拋物線的標準方程;
(2)求![]() 的最小值及此時點
的最小值及此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C:x2=2py經過點(2,1).
(Ⅰ)求拋物線C的方程及其準線方程;
(Ⅱ)設O為原點,過拋物線C的焦點作斜率不為0的直線l交拋物線C于兩點M,N,直線y=1分別交直線OM,ON于點A和點B.求證:以AB為直徑的圓經過y軸上的兩個定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐PABCD中,AD∥BC,平面PAC⊥平面ABCD,AB=AD=DC=1,
∠ABC=∠DCB=60,E是PC上一點.
(Ⅰ)證明:平面EAB⊥平面PAC;
(Ⅱ)若△PAC是正三角形,且E是PC中點,求三棱錐AEBC的體積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com