
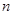 位學生,每次活動均需該系
位學生,每次活動均需該系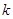 位學生參加(
位學生參加(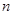 和
和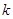 都是固定的正整數)。假設李老師和張老師分別將各自活動通知的信息獨立、隨機地發給該系
都是固定的正整數)。假設李老師和張老師分別將各自活動通知的信息獨立、隨機地發給該系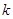 位學生,且所發信息都能收到。記該系收到李老師或張老師所發活動通知信息的學生人數為
位學生,且所發信息都能收到。記該系收到李老師或張老師所發活動通知信息的學生人數為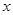
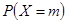 取得最大值的整數
取得最大值的整數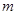 。
。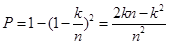 (2)見解析
(2)見解析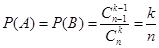 ,沒有收到信息的概率正好是
,沒有收到信息的概率正好是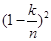 ,所以最后的結果就能求出;第(2)題考查的考點比較多,而且
,所以最后的結果就能求出;第(2)題考查的考點比較多,而且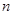 和
和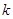 都是變量,遇到變量就要做好討論的準備,于是本題要從
都是變量,遇到變量就要做好討論的準備,于是本題要從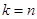 和
和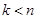 兩個角度考慮.當
兩個角度考慮.當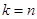 時,
時,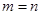 ,
,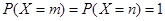 ;當
;當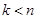 時,整數
時,整數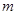 滿足
滿足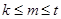 ,其中
,其中 是
是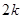 和
和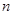 中的較小者,從而表示出
中的較小者,從而表示出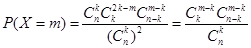 ,接著要根據題意找出不等關系:
,接著要根據題意找出不等關系: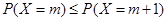 ,化簡分離出
,化簡分離出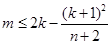 ,而
,而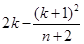 是否為整數,需要討論,還需要考慮
是否為整數,需要討論,還需要考慮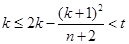 是否成立的問題,于是,接下來一方面需要討論是否為整,另一方面要證明
是否成立的問題,于是,接下來一方面需要討論是否為整,另一方面要證明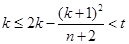 ,詳細的解答如下.
,詳細的解答如下.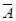 與
與 相互獨立,
相互獨立,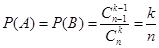

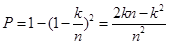 .
.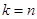 時,
時,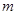 只能取
只能取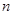 ,有
,有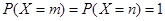
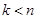 ,整數
,整數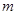 滿足
滿足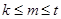 ,其中
,其中 是
是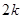 和
和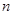 中的較小者.“李老師和張老師各自獨立、隨機地發活動通知信息給
中的較小者.“李老師和張老師各自獨立、隨機地發活動通知信息給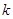 位同學”所包含的基本事件總數為
位同學”所包含的基本事件總數為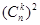 .
.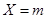 時,同時收到李老師和張老師轉發信息的學生人數恰為
時,同時收到李老師和張老師轉發信息的學生人數恰為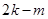 ,僅收到李老師或僅收到張老師轉發信息的學生人數為
,僅收到李老師或僅收到張老師轉發信息的學生人數為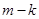 ,則由乘法計數原理知:事件
,則由乘法計數原理知:事件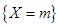 所含基本事件數為
所含基本事件數為
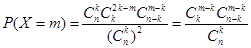
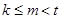 ,
,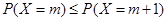
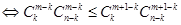
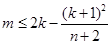
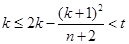 成立,
成立,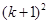 能被
能被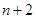 整除時,
整除時,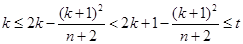 ,故
,故 在
在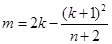 和
和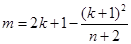 處達到最大值;
處達到最大值;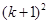 不能被
不能被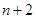 整除時,
整除時, 在
在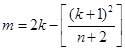 處達最大值.(注:
處達最大值.(注: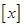 表示不超過
表示不超過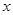 的最大整數).
的最大整數).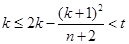
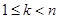 ,所以
,所以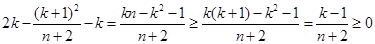 ,
, ,故
,故 ,顯然
,顯然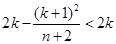 .
.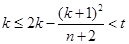 .
.

科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 ,然后再放回箱子中;第二次再從箱子中任取一張卡片,記下它的標號
,然后再放回箱子中;第二次再從箱子中任取一張卡片,記下它的標號 ,求使得冪函數
,求使得冪函數 圖像關于
圖像關于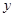 軸對稱的概率.
軸對稱的概率.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
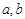 ,按以下程序進行運算:
,按以下程序進行運算: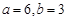 ,求程序運行后計算機輸出的y的值;
,求程序運行后計算機輸出的y的值;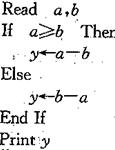
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com