
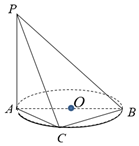
 如圖,AB是⊙O的直徑,P是⊙O所在平面外一點,PA垂直于⊙O所在平面,且PA=AB=10,設(shè)點C為⊙O上異于A、B的任意一點.
如圖,AB是⊙O的直徑,P是⊙O所在平面外一點,PA垂直于⊙O所在平面,且PA=AB=10,設(shè)點C為⊙O上異于A、B的任意一點.分析 (1)由圓的性質(zhì)得AC⊥BC,由線面垂直得BC⊥PA,由此能證明BC⊥平面PAC.
(2)由勾股和得BC=8,推導出平面PAB⊥平面ABC,從而點C到AB的距離d即為點C到平面PAB的距離,由此能求出三棱錐C-PAB的體積.
解答 證明:(1)∵AB是⊙O的直徑,點C為⊙O上異于A、B的任意一點,
∴AC⊥BC,
∵P是⊙O所在平面外一點,PA垂直于⊙O所在平面,BC?⊙O所在平面,
∴BC⊥PA,
∵AC∩PA=A,
∴BC⊥平面PAC.
解:(2)∵AC=6,PA=AB=10,
∴BC=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∵PA垂直于⊙O所在平面,∴PA⊥平面ABC,
又PA?平面PAB,∴平面PAB⊥平面ABC,
∴點C到AB的距離d即為點C到平面PAB的距離,
∵$\frac{1}{2}AB•d$=$\frac{1}{2}AC•BC$,
∴d=$\frac{AC•BC}{AB}$=$\frac{6×8}{10}$=$\frac{24}{5}$,
又S△PAB=$\frac{1}{2}×PA×AB=\frac{1}{2}×10×10$=50,
∴三棱錐C-PAB的體積V=$\frac{1}{3}×{S}_{△PAB}×d$=$\frac{1}{3}×50×\frac{24}{5}$=80.
點評 本題考查線面垂直的證明,考查三棱錐的體積的求法,是中檔題,解題時要認真審題,注意空間思維能力的培養(yǎng).


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:高中數(shù)學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | -1 | D. | 3 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | 雙曲線 | B. | 雙曲線的一支 | C. | 橢圓 | D. | 拋物線 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | l1∥α | B. | l2⊥α | C. | l2∥α或l2?α | D. | l2與α相交 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com