Question

已知直線l:y=ax-1,雙曲線C:3x²-y²=1.

(1)若l與C總有兩個公共點,求a的取值范圍;

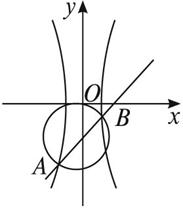
(2)若l與C交于點A、B,且以AB為直徑的圓過原點,求a.

Answer 1

解:由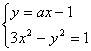(3-a²)x²+2ax-2=0.

(1)若直線l與曲線C總有兩個公共點,則3-a²≠0,且4a²+8(3-a²)=-4(a²-6)＞0,

即a²-6＜0,∴-＜a＜,且a≠±3,

即a的取值范圍為(-,-)∪(-,)∪(3,).

(2)如圖所示,設l與C的交點A、B的坐標分別為(x₁,y₁)、(x₂,y₂),由韋達定理可得:x₁+x₂=,

x₁x₂=.

∴y₁y₂=(ax₁-1)(ax₂-1)=a²x₁x₂-a(x₁+x₂)+1=1.

∵以AB為直徑的圓經過坐標原點,則OA⊥OB,即·=-1,也就是x₁x₂+y₁y₂=0,

∴1=0.∴a=1,或a=-1.

結合(1)可知,當a=±1時,以AB為直徑的圓經過坐標原點.