
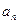 }的前n項和為
}的前n項和為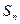 ,并且滿足
,并且滿足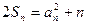 ,
,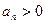 (n∈N*).
(n∈N*).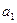 ,
,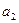 ,
,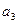 ;
;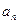 }的通項公式,并用數(shù)學(xué)歸納法加以證明;
}的通項公式,并用數(shù)學(xué)歸納法加以證明;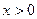 ,
,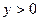 ,且
,且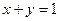 ,證明:
,證明: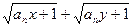 ≤
≤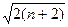 .
. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
 ,
, 可被5整除,那么
可被5整除,那么 中至少有一個能被5整除”,則假設(shè)內(nèi)容是_____________________________________________________.
中至少有一個能被5整除”,則假設(shè)內(nèi)容是_____________________________________________________.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
 ,如果
,如果 可被5整除,那么
可被5整除,那么 ,
, 至少有1個能被5整除.”則假設(shè)的內(nèi)容是 ( )
至少有1個能被5整除.”則假設(shè)的內(nèi)容是 ( )A. , , 都能被5整除 都能被5整除 | B. , , 都不能被5整除 都不能被5整除 |
C. 不能被5整除 不能被5整除 | D. , , 有1個不能被5整除 有1個不能被5整除 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
 ,求證:
,求證: ,用反證法證明時,可假設(shè)
,用反證法證明時,可假設(shè) ;
; ,
, ,求證:方程
,求證:方程 的兩根的絕對值都小于1.用反證法證明時可假設(shè)方程有一根
的兩根的絕對值都小于1.用反證法證明時可假設(shè)方程有一根 的絕對值大于或等于1,即假設(shè)
的絕對值大于或等于1,即假設(shè) ,以下結(jié)論正確的是( )
,以下結(jié)論正確的是( )A. 與 與 的假設(shè)都錯誤 的假設(shè)都錯誤 |
B. 與 與 的假設(shè)都正確 的假設(shè)都正確 |
C. 的假設(shè)正確; 的假設(shè)正確; 的假設(shè)錯誤 的假設(shè)錯誤 |
D. 的假設(shè)錯誤; 的假設(shè)錯誤; 的假設(shè)正確 的假設(shè)正確 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
 …
… >
> (n∈N*,且n>2)時,第二步由
(n∈N*,且n>2)時,第二步由A. | B. + + - -  |
C. + + | D. - -  |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com