
如圖,在四面體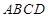 中,
中,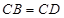 ,
,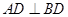 ,點
,點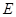 ,
,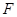 分別是
分別是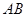 ,
,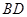 的中點.
的中點.

(1)EF∥平面ACD;
(2)求證:平面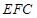 ⊥平面
⊥平面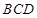 ;
;
(3)若平面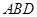 ⊥平面
⊥平面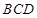 ,且
,且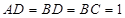 ,求三棱錐
,求三棱錐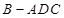 的體積.
的體積.
(1)詳見解析;(2)詳見解析;(3)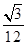
【解析】
試題分析:(1)由直線和平面平行的判定定理,只需在平面內(nèi)找一條直線與平面外直線平行,由 是
是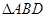 的中位線,知
的中位線,知 ∥
∥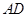 ;(2)由平面和平面垂直的判定定理,只需在一個平面內(nèi)找另一個平面的垂線即可,由
;(2)由平面和平面垂直的判定定理,只需在一個平面內(nèi)找另一個平面的垂線即可,由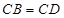 且
且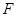 是
是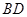 的中點,可得
的中點,可得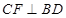 ,又
,又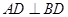 且
且 ∥
∥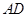 ,知
,知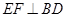 ,且
,且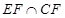 =
=
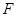 ,所以
,所以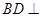 面
面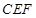 ,又
,又 面
面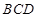 ,從而平面
,從而平面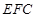 ⊥平面
⊥平面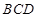 ;(3)由已知面
;(3)由已知面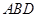 ⊥平面
⊥平面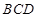 ,則在一個平面內(nèi)垂直于交線的直線,必垂直于另一個平面,由面
,則在一個平面內(nèi)垂直于交線的直線,必垂直于另一個平面,由面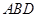
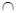 平面
平面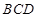 =
=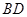 ,且
,且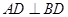 ,所以
,所以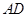
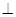 面
面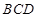 ,∴
,∴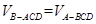 ,只需求
,只需求 的面積即可.
的面積即可.
試題解析:(1)∵EF是△BAD的中位線,所以EF∥AD(2分),又EF⊄平面ACD,AD⊂平面ACD
∴EF∥平面ACD;
(2)∵EF∥AD,AD⊥BD,∴BD⊥EF,又∵BD⊥CF∴BD⊥面CEF,又BD⊂面BDC,∴面EFC⊥面BCD;
(3)因為面ABD⊥面BCD,且AD⊥BD,所以AD⊥面BCD,由BD=BC=1和CB=CD得△BCD是正三角形,所以 .
.
考點:1、直線和平面平行的判定定理;2、面面垂直的判定和性質(zhì)定理;3、幾何體的體積.


科目:高中數(shù)學(xué) 來源: 題型:
如圖,在四面體![]() 中,截面
中,截面![]() 是正方形,則下列命題:
是正方形,則下列命題:
①![]() .②
.②![]() ∥截面
∥截面![]() .③異面直線
.③異面直線![]() 與
與![]() 所成的角為
所成的角為![]() .
.
其中,正確的有 ( )
A.0個 B.1個 C.2個 D.3個
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:山東省曲阜一中10-11學(xué)年高二下學(xué)期期末考試數(shù)學(xué)(理) 題型:解答題
(本小題滿分12分)如圖,在四面體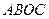 中,
中,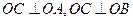 ,
,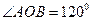 ,且
,且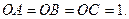
(I)設(shè)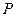 為線段
為線段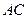 的中點,試在線段
的中點,試在線段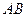 上求一點
上求一點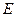 ,使得
,使得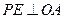
 ;
;
(II)求二面角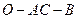 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011年福建省龍巖市高一上學(xué)期期末考試數(shù)學(xué)試卷 題型:選擇題
如圖,在四面體 中,截面
中,截面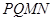 是正方形,則在下列命題中,錯誤的為(
)
是正方形,則在下列命題中,錯誤的為(
)
A. 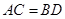
B.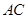 ∥截面
∥截面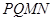
C. 異面直線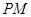 與
與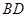 所成的角為
所成的角為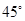
D. 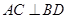
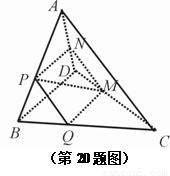
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:廣州省2009-2010學(xué)年高一學(xué)科競賽 題型:解答題
如圖:在四面體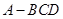 中,
中,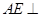 平面
平面
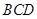 ,
,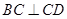 ,
,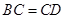 ,
,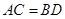 ,
,
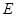 是
是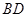 的中點;
的中點;
(1)求證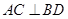 ;
;
(2)求直線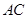 與平面
與平面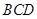 所成的角。
所成的角。
 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com