
已知 ,
,
(Ⅰ)當 時,求曲線
時,求曲線 在點
在點 處的切線方程;
處的切線方程;
(Ⅱ)若 在
在 處有極值,求
處有極值,求 的單調遞增區間;
的單調遞增區間;
(Ⅲ)是否存在實數 ,使
,使 在區間
在區間 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,說明理由.
的值;若不存在,說明理由.
(Ⅰ)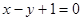 (Ⅱ)
(Ⅱ)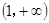 (Ⅲ)
(Ⅲ)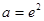
【解析】
試題分析:(Ⅰ)求曲線在一點處的切線方程,一要抓切點(1,2),一要抓導數的幾何意義即切線的斜率 ,便求出切線方程
,便求出切線方程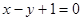 ;(Ⅱ)先利用極值求出系數
;(Ⅱ)先利用極值求出系數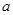 ,再利用
,再利用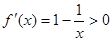 及定義域
及定義域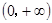 ,求出單調遞增區間為
,求出單調遞增區間為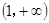 ;(Ⅲ)利用導數求某區間上的最值,要綜合應用極值、單調性進行判定求解,特別對
;(Ⅲ)利用導數求某區間上的最值,要綜合應用極值、單調性進行判定求解,特別對 的形式、
的形式、 的根進行分類討論.多見于單調函數、單峰(谷)函數.
的根進行分類討論.多見于單調函數、單峰(谷)函數.
試題解析:(Ⅰ)函數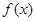 的定義域為
的定義域為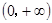 ,
因為
,
因為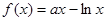 ,所以
,所以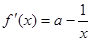
當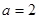 時,
時,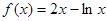 ,
,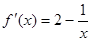 ,所以
,所以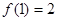 ,
,
所以曲線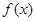 在點
在點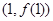 處的切線方程為
處的切線方程為 ,即
,即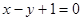 .
3分
.
3分
(Ⅱ)因為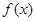 在
在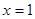 處有極值,所以
處有極值,所以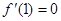 ,
由(Ⅰ)知
,
由(Ⅰ)知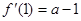 ,所以
,所以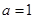
經檢驗,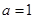 時
時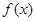 在
在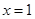 處有極值.
4分
處有極值.
4分
所以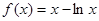 ,令
,令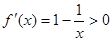 ,解得
,解得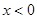 或
或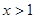 ;
;
因為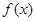 的定義域為
的定義域為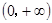 ,所以
,所以 的解集為
的解集為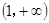 ,
,
即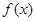 的單調遞增區間為
的單調遞增區間為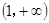 .
6分
.
6分
(Ⅲ)假設存在實數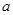 ,使
,使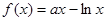 在區間
在區間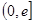 上有最小值3,由
上有最小值3,由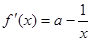 ,
,
① 當 時,
時,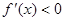 ,
,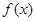 在
在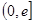 上單調遞減,
上單調遞減,
 ,解得
,解得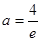 ,舍去.
8分
,舍去.
8分
②當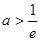 即
即 時,
時,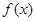 在
在 上單調遞減,在
上單調遞減,在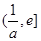 上單調遞增,
上單調遞增,
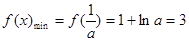 ,解得
,解得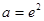 ,滿足條件.
10分
,滿足條件.
10分
③ 當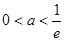 即
即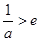 時,
時,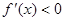 ,
,
所以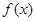 在
在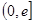 上單調遞減,
上單調遞減, ,解得
,解得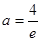 ,舍去.
,舍去.
綜上,存在實數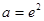 ,使
,使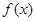 在區間
在區間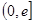 上的最小值是3. 12分
上的最小值是3. 12分
考點:導數的幾何意義 導數的應用 分類討論思想


科目:高中數學 來源: 題型:
三、解答題(本大題共4小題,共50分。解答應寫出文字說明,證明過程或演算步驟)
17.(本小題14分)已知向量![]()
(1)當![]() 時,求
時,求![]() 值的集合;
值的集合;
(2)設函數![]() ① 求
① 求![]() 的最小正周期 ② 寫出函數
的最小正周期 ② 寫出函數![]() 的單調增區間;
的單調增區間;
③ 寫出函數![]() 的圖象的對稱軸方程。
的圖象的對稱軸方程。
查看答案和解析>>
科目:高中數學 來源:2012-2013學年遼寧省沈陽市高三高考領航考試(四)文科數學試卷(解析版) 題型:解答題
(本小題滿分10分)選修4-5:不等式選講
已知函數 .
.
(Ⅰ)當 時,求函數
時,求函數 的定義域;
的定義域;
(Ⅱ)若關于 的不等式
的不等式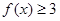 的解集是
的解集是 ,求
,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年浙江省臺州市四校高三第一次聯考理科數學試卷 題型:解答題
(本題滿分14分)
已知集合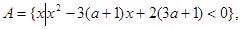
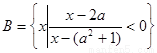 ,
,
(Ⅰ)當 時,求
時,求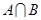 ;
;
(Ⅱ)求使 的實數
的實數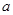 的取值范圍。
的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com