
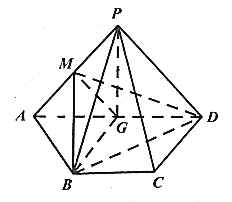
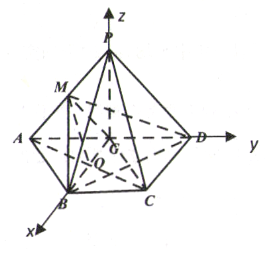
【題目】如圖,已知四邊形![]() 的直角梯形,
的直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 為線段
為線段![]() 的中點,
的中點,![]() 平面
平面![]() ,
,![]() ,
,![]() 為線段
為線段![]() 上一點(
上一點(![]() 不與端點重合).
不與端點重合).
(Ⅰ)若![]() ,
,
(i)求證:![]() 平面
平面![]() ;
;
(ii)求直線![]() 與平面
與平面![]() 所成的角的大小;
所成的角的大小;
(Ⅱ)否存在實數![]() 滿足
滿足![]() ,使得平面
,使得平面![]() 與平面
與平面![]() 所成的銳角為
所成的銳角為![]() ,若存在,確定
,若存在,確定![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
【答案】(Ⅰ)(i)見解析(ii)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)(i)先根據平行四邊形性質得![]() ,再根據線面平行判定定理得結果,(ii)先根據條件建立空間直角坐標系,設立各點坐標,列方程組解得平面
,再根據線面平行判定定理得結果,(ii)先根據條件建立空間直角坐標系,設立各點坐標,列方程組解得平面![]() 的法向量,根據向量數量積得向量夾角,最后根據線面角與向量夾角關系得結果.(Ⅱ)先根據條件建立空間直角坐標系,設立各點坐標,列方程組解得兩平面法向量,根據向量數量積得向量夾角,最后根據二面角與向量夾角關系得結果.
的法向量,根據向量數量積得向量夾角,最后根據線面角與向量夾角關系得結果.(Ⅱ)先根據條件建立空間直角坐標系,設立各點坐標,列方程組解得兩平面法向量,根據向量數量積得向量夾角,最后根據二面角與向量夾角關系得結果.
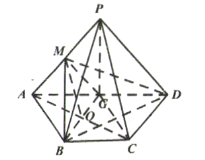
(Ⅰ)(i)證明:連接![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,
,![]() ,依題意易證四邊形
,依題意易證四邊形![]() 為平行四邊形.
為平行四邊形.
∴![]() 又∵
又∵![]() ,
,
∴![]() 又∵
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(ii)解:如圖,在平行四邊形![]() 中∵
中∵![]() ,
,![]() ,∴
,∴![]()
以![]() 為原點建立空間直角坐標系
為原點建立空間直角坐標系![]()
則![]() ,
,
![]()
∴![]()
設![]() 為平面
為平面![]() 的法向量
的法向量
則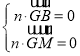 ,得
,得![]() ,不妨設
,不妨設![]()
∴![]()
又![]() ,∴
,∴![]()
即直線![]() 與平面
與平面![]() 所成的角的大小為
所成的角的大小為![]() .
.
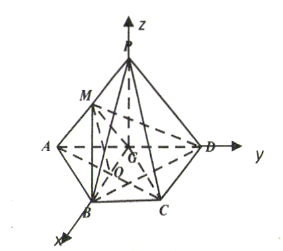
(Ⅱ)設![]()
∴![]()
∴![]()
設![]() 為平面
為平面![]() 的法向量,
的法向量,
則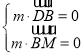 得,
得,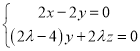 ,不妨設
,不妨設![]() ,
,
又平面![]() 的法向量為
的法向量為![]() ,
,
∴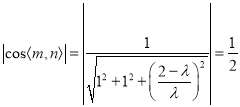 .
.
∴![]() ∴
∴![]() ,
,![]() ,∴
,∴![]() .
.


科目:高中數學 來源: 題型:
【題目】江夏一中將要舉行校園歌手大賽,現有3男3女參加,需要安排他們的出場順序.(結果用數字作答)
(1)如果3個女生都不相鄰,那么有多少種不同的出場順序?
(2)如果女生甲在女生乙的前面(可以不相鄰),那么有多少種不同的出場順序?
(3)如果3位男生都相鄰,且女生甲不在第一個出場,那么有多少種不同的出場順序?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校在2012年的自主招生考試成績中隨機抽取![]() 名中學生的筆試成績,按成績分組,得到的頻率分布表如表所示.
名中學生的筆試成績,按成績分組,得到的頻率分布表如表所示.
組號 | 分組 | 頻數 | 頻率 |
第1組 |
| 5 |
|
第2組 |
| ① |
|
第3組 |
| 30 | ② |
第4組 |
| 20 |
|
第5組 |
| 10 |
|

(1)請先求出頻率分布表中![]() 位置的相應數據,再完成頻率分布直方圖;
位置的相應數據,再完成頻率分布直方圖;
(2)為了能選拔出最優秀的學生,高校決定在筆試成績高的第![]() 組中用分層抽樣抽取名學生進入第二輪面試,求第3、4、5組每組各抽取多少名學生進入第二輪面試;
組中用分層抽樣抽取名學生進入第二輪面試,求第3、4、5組每組各抽取多少名學生進入第二輪面試;
(3)在(2)的前提下,學校決定在![]() 名學生中隨機抽取
名學生中隨機抽取![]() 名學生接受
名學生接受![]() 考官進行面試,求:第
考官進行面試,求:第![]() 組至少有一名學生被考官
組至少有一名學生被考官![]() 面試的概率.
面試的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年2月13日《煙臺市全民閱讀促進條例》全文發布,旨在保障全民閱讀權利,培養全民閱讀習慣,提高全民閱讀能力,推動文明城市和文化強市建設.某高校為了解條例發布以來全校學生的閱讀情況,隨機調查了200名學生每周閱讀時間![]() (單位:小時)并繪制如圖所示的頻率分布直方圖.
(單位:小時)并繪制如圖所示的頻率分布直方圖.
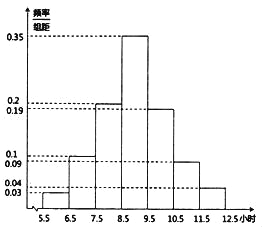
(1)求這200名學生每周閱讀時間的樣本平均數![]() 和樣本方差
和樣本方差![]() (同一組中的數據用該組區間的中間值代表);
(同一組中的數據用該組區間的中間值代表);
(2)由直方圖可以認為,目前該校學生每周的閱讀時間![]() 服從正態分布
服從正態分布![]() ,其中
,其中![]() 近似為樣本平均數
近似為樣本平均數![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() .
.
(i)一般正態分布的概率都可以轉化為標準正態分布的概率進行計算:若![]() ,令
,令![]() ,則
,則![]() ,且
,且![]() .利用直方圖得到的正態分布,求
.利用直方圖得到的正態分布,求![]() .
.
(ii)從該高校的學生中隨機抽取20名,記![]() 表示這20名學生中每周閱讀時間超過10小時的人數,求
表示這20名學生中每周閱讀時間超過10小時的人數,求![]() (結果精確到0.0001)以及
(結果精確到0.0001)以及![]() 的數學期望.
的數學期望.
參考數據:![]() ,
,![]() .若
.若![]() ,則
,則![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com