
分析 (Ⅰ)利用三種方程互化方法,將曲線C和直線l化為直角坐標方程;
(Ⅱ)由于點Q是曲線C上的點,則可設點Q的坐標為($\sqrt{3}$cosθ,sinθ),利用點到直線的距離公式,求它到直線l的距離的最大值.
解答 解:(Ⅰ)由曲線C的參數方程為$\left\{\begin{array}{l}{x=\sqrt{3}cosθ}\\{y=sinθ}\end{array}\right.$(θ為參數)得$\frac{{x}^{2}}{3}+{y}^{2}$=1,
∴曲線C的直角坐標方程為$\frac{{x}^{2}}{3}+{y}^{2}$=1.…(2分)
由ρsin(θ+$\frac{π}{4}$)=$\sqrt{2}$,化簡得,ρsinθ+ρcosθ=2,…(4分)
∴x+y=2.
∴直線l的直角坐標方程為x+y=2.…(5分)
(Ⅱ)由于點Q是曲線C上的點,則可設點Q的坐標為($\sqrt{3}$cosθ,sinθ),…(6分)
點Q到直線l的距離為d=$\frac{|\sqrt{3}cosθ+sinθ-2|}{\sqrt{2}}$…(7分)
=$\frac{|2cos(θ-\frac{π}{6})-2|}{\sqrt{2}}$.…(8分)
當cos(θ-$\frac{π}{6}$)=-1時,dmax=2$\sqrt{2}$.…(9分)
∴點Q到直線l的距離的最大值為2$\sqrt{2}$.…(10分)
點評 本題考查三種方程的互化,考查點到直線的距離公式的運用,考查參數方程,屬于中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\sqrt{13}$ | C. | 13 | D. | $\sqrt{7-2\sqrt{3}}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{5}{12}$ | B. | $\frac{7}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x1>x2 | B. | x1>|x2| | C. | x1<x2 | D. | x${\;}_{1}^{2}$>x${\;}_{2}^{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {2,3,4,5} | B. | {-1,0} | C. | {-1,0,1,2} | D. | { 2,3,4} |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
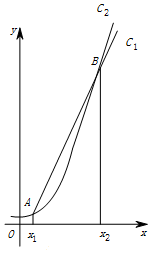 函數f(x)=2x和g(x)=x3的圖象的示意圖如圖所示,設兩函數的圖象交于點A(x1,y1),B(x2,y2),且x1<x2.若x1∈[a,a+1],x2∈[b,b+1],且a,b∈{1,2,3,4,5,6,7,8,9,10,11,12},則a+b=10.
函數f(x)=2x和g(x)=x3的圖象的示意圖如圖所示,設兩函數的圖象交于點A(x1,y1),B(x2,y2),且x1<x2.若x1∈[a,a+1],x2∈[b,b+1],且a,b∈{1,2,3,4,5,6,7,8,9,10,11,12},則a+b=10.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com