
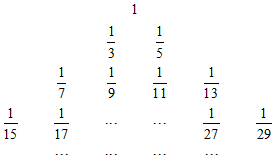
分析 第k行有2k-1個(gè)數(shù)知每行數(shù)的個(gè)數(shù)成等比數(shù)列,要求A(t,s),先求A(t,1),就必須求出前t-1行一共出現(xiàn)了多少個(gè)數(shù),根據(jù)等比數(shù)列求和公式可求,而由$\frac{1}{2n-1}$可知,每一行數(shù)的分母成等差數(shù)列,可求A(t,s),令t=11,s=4,可求A(11,4).
解答 解:由第k行有2k-1個(gè)數(shù),知每一行數(shù)的個(gè)數(shù)構(gòu)成等比數(shù)列,首項(xiàng)是1,公比是2,
∴前t-1行共有$\frac{1-{2}^{t-1}}{1-2}$=2t-1-1個(gè)數(shù),
∴第t行第一個(gè)數(shù)是A(t,1)=$\frac{1}{2•{2}^{t-1}-1}$=$\frac{1}{{2}^{t}-1}$,
∴A(t,s)=$\frac{1}{{2}^{t}-1+2(s-1)}$,
令t=11,s=4,
∴A(11,4)=$\frac{1}{2053}$.
故答案為$\frac{1}{2053}$.
點(diǎn)評 本題考查數(shù)列的性質(zhì)和應(yīng)用,解題時(shí)要注意數(shù)表的合理運(yùn)用,解題時(shí)要認(rèn)真審題,仔細(xì)解答.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $y={x^{\frac{2}{3}}}$ | B. | $y={x^{-\frac{1}{3}}}$ | C. | $y={x^{\frac{3}{2}}}$ | D. | $y={x^{-\frac{2}{3}}}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | [1,+∞) | B. | (1,+∞) | C. | [2,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 1:2:3 | B. | $1:\sqrt{2}:\sqrt{3}$ | C. | $1:\sqrt{3}:2$ | D. | $2:\sqrt{3}:4$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
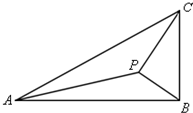 如圖,在△ABC中,∠ABC=90°,AB=$\sqrt{3}$,BC=1,P為△ABC內(nèi)一點(diǎn),∠BPC=90°.
如圖,在△ABC中,∠ABC=90°,AB=$\sqrt{3}$,BC=1,P為△ABC內(nèi)一點(diǎn),∠BPC=90°.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com