
已知函數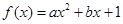 (
(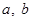 為實數,
為實數,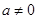 ,
,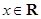 ),
),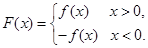
(Ⅰ)若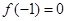 ,且函數
,且函數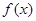 的值域為
的值域為 ,求
,求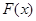 的表達式;
的表達式;
(Ⅱ)在(Ⅰ)的條件下,當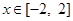 時,
時, 是單調函數,求實數
是單調函數,求實數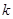 的取值范圍;
的取值范圍;
(Ⅲ)設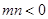 ,
,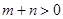 ,
,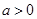 ,且函數
,且函數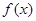 為偶函數,判斷
為偶函數,判斷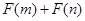 是否大于
是否大于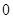 ?
?
科目:高中數學 來源: 題型:解答題
某工廠某種產品的年固定成本為250萬元,每生產 千件,需另投入成本為
千件,需另投入成本為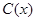 ,當年產量不足80千件時,
,當年產量不足80千件時, (萬元).當年產量不小于80千件時,
(萬元).當年產量不小于80千件時, (萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產的商品能全部售完.
(萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產的商品能全部售完.
(Ⅰ)寫出年利潤 (萬元)關于年產量
(萬元)關于年產量 (千件)的函數解析式;
(千件)的函數解析式;
(Ⅱ)年產量為多少千件時,該廠在這一商品的生產中所獲利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
隨著機構改革工作的深入進行,各單位要減員增效。有一家公司現有職員 人,(
人,( ,且
,且 為偶數),每人每年可創利
為偶數),每人每年可創利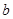 萬元。據評估,在經營條件不變的前提下,每裁員1人,則留崗職員每人每年可多創利
萬元。據評估,在經營條件不變的前提下,每裁員1人,則留崗職員每人每年可多創利 萬元,但公司需支付下崗職員每人每年
萬元,但公司需支付下崗職員每人每年 萬元的生活費,并且該公司正常運轉所需人數不得小于現有員工的
萬元的生活費,并且該公司正常運轉所需人數不得小于現有員工的 ,為獲得最大的經濟效益,該公司應裁員多少人?
,為獲得最大的經濟效益,該公司應裁員多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知二次函數f(x)滿足條件f(0)=1和f(x+1)-f(x)=2x.
(1)求f(x);
(2)求f(x)在區間[-1,1]上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對于在區間 [ m,n ] 上有意義的兩個函數 與
與 ,如果對任意
,如果對任意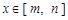 ,均有
,均有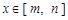 ,則稱
,則稱 與
與 在 [ m,n ] 上是友好的,否則稱
在 [ m,n ] 上是友好的,否則稱 與
與 在 [ m,n ]是不友好的.現有兩個函數
在 [ m,n ]是不友好的.現有兩個函數 與
與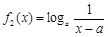 (a > 0且
(a > 0且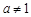 ),給定區間
),給定區間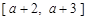 .
.
(1)若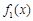 與
與 在給定區間
在給定區間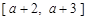 上都有意義,求a的取值范圍;
上都有意義,求a的取值范圍;
(2)討論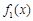 與
與 在給定區間
在給定區間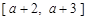 上是否友好.
上是否友好.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
進貨原價為80元的商品400個,按90元一個售出時,可全部賣出.已知這種商品每個漲價一元,其銷售數就減少20個,問售價應為多少時所獲得利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知冪函數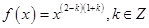 ,且
,且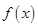 在
在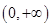 上單調遞增.
上單調遞增.
(1)求實數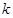 的值,并寫出相應的函數
的值,并寫出相應的函數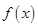 的解析式;
的解析式;
(2)若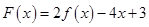 在區間
在區間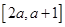 上不單調,求實數
上不單調,求實數 的取值范圍;
的取值范圍;
(3)試判斷是否存在正數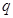 ,使函數
,使函數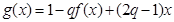 在區間
在區間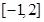 上的值域為
上的值域為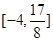 若存在,求出
若存在,求出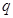 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知二次函數f(x)有兩個零點0和-2,且f(x)最小值是-1,函數g(x)與f(x)的圖像關于原點對稱.
(1)求f(x)和g(x)的解析式;
(2)若h(x)=f(x)-λg(x)在區間[-1,1]上是增函數,求實數λ的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com