
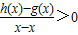 在D內恒成立,則稱P為函數y=h(x)的“類對稱點”,當a=4時,試問y=f(x)是否存在“類對稱點”,若存在,請至少求出一個“類對稱點”的橫坐標,若不存在,說明理由.
在D內恒成立,則稱P為函數y=h(x)的“類對稱點”,當a=4時,試問y=f(x)是否存在“類對稱點”,若存在,請至少求出一個“類對稱點”的橫坐標,若不存在,說明理由.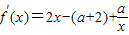 =
=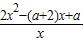 =
=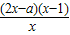 ,能求出當a>2時,求函數f(x)的單調遞增區間.
,能求出當a>2時,求函數f(x)的單調遞增區間.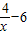 ,故
,故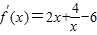 ≥4
≥4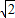 -6,不存在6x+y+m=0這類直線的切線.
-6,不存在6x+y+m=0這類直線的切線.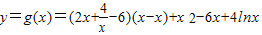 ,令h(x)=f(x)-g(x),由此入手,能夠求出一個“類對稱點”的橫坐標.
,令h(x)=f(x)-g(x),由此入手,能夠求出一個“類對稱點”的橫坐標.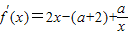 =
=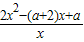 =
=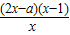 ,
,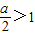 .
.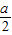 時,f′(x)>0.當1<x<
時,f′(x)>0.當1<x< 時,f′(x)<0,
時,f′(x)<0, ).
). ,
,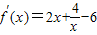 ≥4
≥4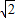 -6,
-6,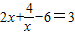 得
得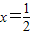 與x=4,當
與x=4,當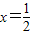 時,求得
時,求得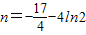 .
. ,
,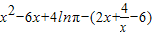 •(x-x)-(
•(x-x)-(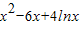 ),
),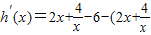 -6)=2(x-x)(1-
-6)=2(x-x)(1-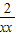 )=
)=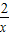 (x-x)(x-
(x-x)(x-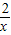 ),
),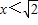 時,h(x)在(x,
時,h(x)在(x,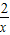 )上單調遞減.
)上單調遞減.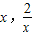 )時,h(x)<h(x)=0,從而有x∈(
)時,h(x)<h(x)=0,從而有x∈(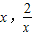 )時,
)時,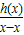 <0,
<0, 時,h(x)在(
時,h(x)在(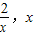 )上單調遞減,
)上單調遞減,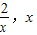 ).
). 時,
時,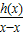 <0.
<0.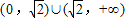 上不存在“類對稱點”.
上不存在“類對稱點”.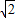 時,
時,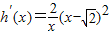 ,
,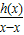 >0,
>0,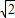 是一個類對稱點的橫坐標.
是一個類對稱點的橫坐標.

科目:高中數學 來源: 題型:
 已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 3 |
| f′(x) |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x |
| a |
| b |
| x |
| 4c2 |
| k(k+c) |
查看答案和解析>>
科目:高中數學 來源:上海模擬 題型:解答題
| x |
| a |
| b |
| x |
| 4c2 |
| k(k+c) |
查看答案和解析>>
科目:高中數學 來源:深圳一模 題型:解答題
| 1 |
| 3 |
| f′(x) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com