
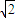 a,0)、B(2
a,0)、B(2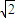 a,0,0)、C(0,2
a,0,0)、C(0,2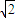 a,0)、P(0,0,2
a,0)、P(0,0,2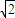 a),設E為BC的中點,連接PE、QE、OE,則∠PEQ=2∠PEO即為所求二面角的平面角;設n=(x,y,z)是AB與PC的公垂線的一個方向向量,則有n•
a),設E為BC的中點,連接PE、QE、OE,則∠PEQ=2∠PEO即為所求二面角的平面角;設n=(x,y,z)是AB與PC的公垂線的一個方向向量,則有n•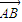 =x+y=0,n•
=x+y=0,n•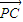 =y-z=0,解得n=(-1,1,1),所以向量
=y-z=0,解得n=(-1,1,1),所以向量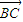 =(-2
=(-2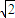 a,2
a,2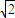 a,0)在n上的射影長d=
a,0)在n上的射影長d=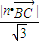 =
=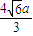 即為所求.
即為所求.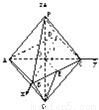 解:如圖,設正八面體的棱長為4a,以中心O為原點,
解:如圖,設正八面體的棱長為4a,以中心O為原點,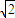 a,0)、B(2
a,0)、B(2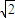 a,0,0)、C(0,2
a,0,0)、C(0,2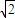 a,0)、
a,0)、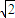 a),設E為BC的中點,連接PE、QE、OE,
a),設E為BC的中點,連接PE、QE、OE,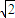 a,
a,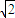 ,∠PEQ=2arctan
,∠PEQ=2arctan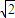 .
.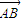 =x+y=0,n•
=x+y=0,n•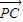 =y-z=0,解得n=(-1,1,1),
=y-z=0,解得n=(-1,1,1),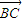 =(-2
=(-2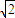 a,2
a,2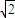 a,0)在n上的射影長d=
a,0)在n上的射影長d=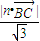 =
=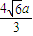 即為所求.
即為所求.

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com