
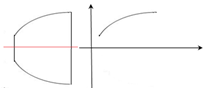
 學完解析幾何和立體幾何后,某同學發現自己家碗的側面可以看做拋物線的一部分曲線圍繞其對稱軸旋轉而成,他很想知道拋物線的方程,決定把拋物線的頂點確定為原點,對稱軸確定為x軸,建立如圖所示的平面直角坐標系,但是他無法確定碗底中心到原點的距離,請你通過對碗的相關數據的測量以及進一步的計算,幫助他求出拋物線的方程.你需要測量的數據是碗底的直徑2m,碗口的直徑2n,碗的高度h(所有測量數據用小寫英文字母表示),算出的拋物線標準方程為y2=$\frac{{n}^{2}-{m}^{2}}{h}$x.
學完解析幾何和立體幾何后,某同學發現自己家碗的側面可以看做拋物線的一部分曲線圍繞其對稱軸旋轉而成,他很想知道拋物線的方程,決定把拋物線的頂點確定為原點,對稱軸確定為x軸,建立如圖所示的平面直角坐標系,但是他無法確定碗底中心到原點的距離,請你通過對碗的相關數據的測量以及進一步的計算,幫助他求出拋物線的方程.你需要測量的數據是碗底的直徑2m,碗口的直徑2n,碗的高度h(所有測量數據用小寫英文字母表示),算出的拋物線標準方程為y2=$\frac{{n}^{2}-{m}^{2}}{h}$x. 分析 碗底的直徑2m,碗口的直徑2n,碗的高度h;設方程為y2=2px(p>0),則將點(a,m),(a+h,n),即可得出結論.
解答 解:碗底的直徑2m,碗口的直徑2n,碗的高度h;
設方程為y2=2px(p>0),則將點(a,m),(a+h,n)
代入拋物線方程可得m2=2pa,n2=2p(a+h),可得2p=$\frac{{n}^{2}-{m}^{2}}{h}$,
∴拋物線方程為y2=$\frac{{n}^{2}-{m}^{2}}{h}$x.
故答案為碗底的直徑2m,碗口的直徑2n,碗的高度h;y2=$\frac{{n}^{2}-{m}^{2}}{h}$x.
點評 本題考查拋物線的方程,考查利用數學知識解決實際問題,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 如果直線m∥平面α,直線n?α內,那么m∥n | |
| B. | 如果平面α⊥平面β,任取直線m?α,那么必有m丄β | |
| C. | 若直線m∥平面α,直線n∥平面α,則m∥n | |
| D. | 如果平面a外的一條直線m垂直于平面a內的兩條相交直線,那么m⊥α |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 已知直棱柱ABC-A1B1C1中,AC=BC=CC1=$\frac{\sqrt{2}}{2}$AB,E是線段CC1的中點,連接AE,B1E,AB1,B1C,BC1,得到的圖形如圖所示.
已知直棱柱ABC-A1B1C1中,AC=BC=CC1=$\frac{\sqrt{2}}{2}$AB,E是線段CC1的中點,連接AE,B1E,AB1,B1C,BC1,得到的圖形如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
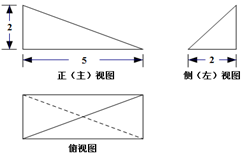
| A. | $\frac{5}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{20}{3}$ | D. | $\frac{25}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,0) | B. | (0,+∞) | C. | $({-∞,\frac{1}{e}})$ | D. | $({\frac{1}{e},+∞})$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com