
已知中心在原點,焦點在 軸上的橢圓
軸上的橢圓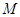 的離心率為
的離心率為 ,橢圓上異于長軸頂點的任意點
,橢圓上異于長軸頂點的任意點 與左右兩焦點
與左右兩焦點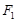 、
、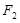 構成的三角形中面積的最大值為
構成的三角形中面積的最大值為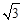 .
.
(1)求橢圓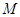 的標準方程;
的標準方程;
(2)已知點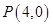 ,連接
,連接 與橢圓的另一交點記為
與橢圓的另一交點記為 ,若
,若 與橢圓相切時
與橢圓相切時 、
、 不重合,連接
不重合,連接 與橢圓的另一交點記為
與橢圓的另一交點記為 ,求
,求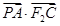 的取值范圍.
的取值范圍.
(1)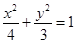 ;(2)
;(2)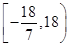 .
.
解析試題分析:(1)先利用已知條件列舉出有關 、
、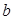 、
、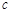 的方程組,結合三者之間滿足的勾股關系求出
的方程組,結合三者之間滿足的勾股關系求出 、
、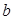 、
、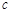 的值,從而確定橢圓的方程;(2)設直線
的值,從而確定橢圓的方程;(2)設直線 與
與 的方程分別為
的方程分別為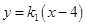 以及
以及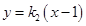 ,將兩條直線方程與橢圓方程聯立,結合韋達定理得到點
,將兩條直線方程與橢圓方程聯立,結合韋達定理得到點 與點
與點 之間的關系(關于
之間的關系(關于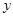 軸對稱),從而得到兩點坐標之間的關系,最后將
軸對稱),從而得到兩點坐標之間的關系,最后將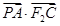 利用點
利用點 的坐標進行表示,注意到坐標的取值范圍,然后利用二次函數求出
的坐標進行表示,注意到坐標的取值范圍,然后利用二次函數求出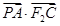 的取值范圍.
的取值范圍.
(1)由題可知: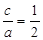 ,
,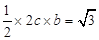 ,
,
解得: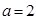 ,
, ,
,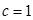 ,
,
故橢圓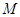 的方程為:
的方程為: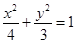 ;
;
(2)不妨設 、
、 、
、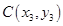 ,
,
由題意可知直線 的斜率是存在的,故設直線
的斜率是存在的,故設直線 的斜率為
的斜率為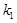 ,直線
,直線 的斜率為
的斜率為
 的方程為: 代入橢圓方程
的方程為: 代入橢圓方程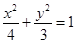 ,得
,得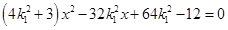 ,
, ,
,
將 ,
, 代入解得:
代入解得: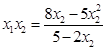 ,
, 的方程為:
的方程為: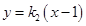 代入橢圓方程
代入橢圓方程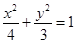 ,得
,得 ,
, ,
,
將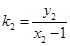 ,
, ,代入解得:
,代入解得: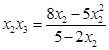 ,
, ,又
,又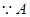 、
、 不重合,
不重合, ,
,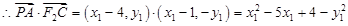
 ,
, .
.
考點:1.橢圓的方程;2.直線與橢圓的位置關系;3.二次函數;4.向量的數量積


 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:高中數學 來源: 題型:解答題
銷售甲、乙兩種商品所得利潤分別為P(單位:萬元)和Q(單位:萬元),它們與投入資金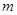 (單位:萬元)的關系有經驗公式
(單位:萬元)的關系有經驗公式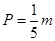 ,
, 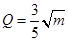 . 今將3萬元資金投入經營甲、乙兩種商品,其中對甲種商品投資
. 今將3萬元資金投入經營甲、乙兩種商品,其中對甲種商品投資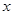 (單位:萬元)
(單位:萬元)
(1)試建立總利潤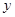 (單位:萬元)關于
(單位:萬元)關于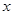 的函數關系式,并指明函數定義域;
的函數關系式,并指明函數定義域;
(2)如何投資經營甲、乙兩種商品,才能使得總利潤最大.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=3x-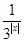 .
.
(1)若f(x)=2,求x的值;
(2)判斷x>0時,f(x)的單調性;
(3)若3tf(2t)+mf(t)≥0對于t∈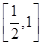 恒成立,求m的取值范圍.
恒成立,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分14分)本題共有2個小題,第1小題滿分6分,第2個小題滿分8分。
已知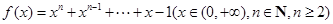 .
.
(1)當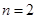 ,
,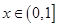 時,若不等式
時,若不等式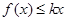 恒成立,求
恒成立,求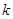 的范圍;
的范圍;
(2)試證函數 在
在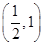 內存在零點.
內存在零點.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了降低能源損耗,某體育館的外墻需要建造隔熱層.體育館要建造可使用20年的隔熱層,每厘米厚的隔熱層建造成本為6萬元.該建筑物每年的能源消耗費用C(單位:萬元)與隔熱層厚度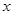 (單位:cm)滿足關系:
(單位:cm)滿足關系: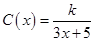 (
(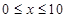 ,
,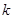 為常數),若不建隔熱層,每年能源消耗費用為8萬元.設
為常數),若不建隔熱層,每年能源消耗費用為8萬元.設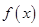 為隔熱層建造費用與20年的能源消耗費用之和.
為隔熱層建造費用與20年的能源消耗費用之和.
(1)求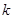 的值及
的值及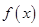 的表達式;
的表達式;
(2)隔熱層修建多厚時,總費用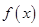 達到最小?并求出最小值.
達到最小?并求出最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了尋找馬航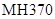 殘骸,我國“雪龍號”科考船于2014年3月26日從港口
殘骸,我國“雪龍號”科考船于2014年3月26日從港口 出發,沿北偏東
出發,沿北偏東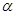 角的射線
角的射線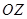 方向航行,而在港口北偏東
方向航行,而在港口北偏東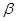 角的方向上有一個給科考船補給物資的小島
角的方向上有一個給科考船補給物資的小島 ,
,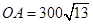 海里,且
海里,且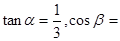
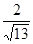 .現指揮部需要緊急征調位于港口
.現指揮部需要緊急征調位于港口 正東
正東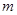 海里的
海里的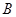 處的補給船,速往小島
處的補給船,速往小島 裝上補給物資供給科考船.該船沿
裝上補給物資供給科考船.該船沿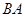 方向全速追趕科考船,并在
方向全速追趕科考船,并在 處相遇.經測算當兩船運行的航線與海岸線
處相遇.經測算當兩船運行的航線與海岸線 圍成的三角形
圍成的三角形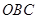 的面積
的面積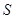 最小時,這種補給方案最優.
最小時,這種補給方案最優.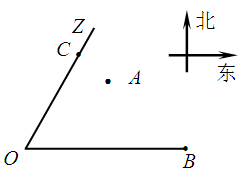
(1)求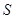 關于
關于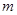 的函數關系式
的函數關系式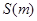 ;
;
(2)應征調位于港口正東多少海里處的補給船只,補給方案最優?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知 的圖象關于坐標原點對稱。
的圖象關于坐標原點對稱。
(1)求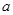 的值,并求出函數
的值,并求出函數 的零點;
的零點;
(2)若函數 在[0,1]內存在零點,求實數b的取值范圍;
在[0,1]內存在零點,求實數b的取值范圍;
(3)設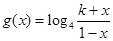 ,已知
,已知 的反函數
的反函數 =
= ,若不等式
,若不等式 在
在 上恒成立,求滿足條件的最小整數k的值。
上恒成立,求滿足條件的最小整數k的值。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
定義在[-1,1]上的奇函數f(x),已知當x∈[-1,0]時,
f(x)=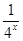 -
-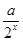 (a∈R).
(a∈R).
(1)求f(x)在[0,1]上的最大值;
(2)若f(x)是[0,1]上的增函數,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com