6
���������cM������(bi��o)��֪�cM���ԣ�2��0����A�ģ��돽��5�Ĵ�A�ϣ��o���ĈAC���cM��܉�E��ͬ�ĈA����
��֪N��܉�E�LjA����M��܉�E�ϣ��돽��1�ĈA�������D�κ����Ì��Q��ȡN��܉�E�cx�S�����c�������õ�Nȡԓ�c�r��ʹ
��ֵ��С��
���
�⣺�O(sh��)M��x��y������M��2+5cos�ȣ�5sin�ȣ�������
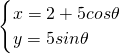
��
�������x-2��
2+y
2=25�����cM��һ���A�Ğ飨2��0�����돽��5�Ĵ�A�ϣ��@����A�c�AC����x-2��
2+y
2=4��ͬ�ĈA��
���cN�M��
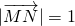
�������cN��܉�E�飨x-2-5cos�ȣ�
2+��y-5sin�ȣ�
2=1��
���ڌ��Q�ԣ��҂�?n��i)�һ���^�鷽���λ���M���о�����D��
ȡ��=0���˕r�AN�ĈA�Ğ飨7��0��������N�c�ڣ�x-7��
2+y
2=1��С�A�ϣ��@��С�A�cx�S�Ѓɂ����c����߅�Ľ��cN
1��6��0������߅�Ľ��cN
2��8��0�������N
1�x�AC���������о���̣��ɗl�о��ĊA�Ǧ�����Ҧ����J�ǣ�cos���ǜp����(sh��)�������N
1�����ăɗl�о�������ģ��С��cos����ֵ��С���ʔ�(sh��)���e
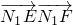
��������
��RT��CEN
1�У�CN
1=4��CE=2����
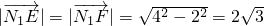
��cos

=

��
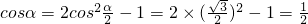
��
��
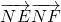
����Сֵ��
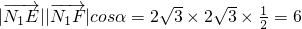
��
�ʴ𰸞�6��
�c�u�����}������ƽ��������(sh��)���e���\�㣬�����ˈA�ą���(sh��)���̣��w�F(xi��n)�˔�(sh��)�νY(ji��)�ϵĽ��}˼�룬�����}���P(gu��n)�I���x���}Ŀ��˼�����Йn�}��

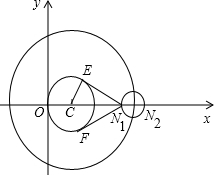
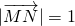 ���^N���AC����x-2��2+y2=4�ăɗl�о�NE��NF�����c�քe��E��F(xi��n)���t
���^N���AC����x-2��2+y2=4�ăɗl�о�NE��NF�����c�քe��E��F(xi��n)���t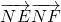 ����Сֵ��________��
����Сֵ��________��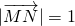 ��֪N��܉�E�LjA����M��܉�E�ϣ��돽��1�ĈA�������D�κ����Ì��Q��ȡN��܉�E�cx�S�����c�������õ�Nȡԓ�c�r��ʹ
��֪N��܉�E�LjA����M��܉�E�ϣ��돽��1�ĈA�������D�κ����Ì��Q��ȡN��܉�E�cx�S�����c�������õ�Nȡԓ�c�r��ʹ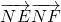 ��ֵ��С��
��ֵ��С�� �⣺�O(sh��)M��x��y������M��2+5cos�ȣ�5sin�ȣ�������
�⣺�O(sh��)M��x��y������M��2+5cos�ȣ�5sin�ȣ�������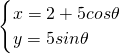 ��
��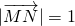 �������cN��܉�E�飨x-2-5cos�ȣ�2+��y-5sin�ȣ�2=1��
�������cN��܉�E�飨x-2-5cos�ȣ�2+��y-5sin�ȣ�2=1��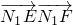 ������С��
��������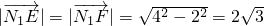 ��cos
��cos =
= ��
��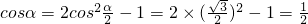 ��
��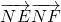 ����Сֵ��
����Сֵ��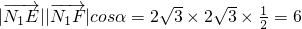 ��
��

 ��У�n��ϵ�д�
��У�n��ϵ�д�
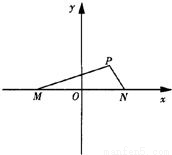
 ��D����֪������(bi��o)ƽ���(n��i)��M��N��x�S���P(gu��n)��ԭ�cO���Q�ă��c��P���ϰ�ƽ���(n��i)һ�c����PMN����e��
��D����֪������(bi��o)ƽ���(n��i)��M��N��x�S���P(gu��n)��ԭ�cO���Q�ă��c��P���ϰ�ƽ���(n��i)һ�c����PMN����e��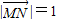 ���^N���AC����x-2��2+y2=4�ăɗl�о�NE��NF�����c�քe��E��F(xi��n)���t
���^N���AC����x-2��2+y2=4�ăɗl�о�NE��NF�����c�քe��E��F(xi��n)���t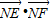 ����Сֵ�� ��
����Сֵ�� ��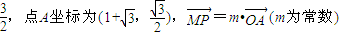 ��
��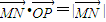 ��
�� ����2�����C����1+��2=0��
����2�����C����1+��2=0��