
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{11}{8}$ | D. | $-\frac{5}{8}$ |
分析 可畫出圖形,并連接AE,從而有AE⊥BC,這便得出$\overrightarrow{AE}•\overrightarrow{BC}=0$,并由條件得出$\overrightarrow{EF}=\frac{1}{2}\overrightarrow{DE}$,而$\overrightarrow{AF}=\overrightarrow{AE}+\overrightarrow{EF}$,代入$\overrightarrow{AF}•\overrightarrow{BC}$,進行數量積的運算即可求出該數量積的值.
解答 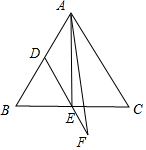 解:如圖,連接AE,則:AE⊥BC;
解:如圖,連接AE,則:AE⊥BC;
$\overrightarrow{DE}=2\overrightarrow{EF}$;
∴$\overrightarrow{EF}=\frac{1}{2}\overrightarrow{DE}$;
∴$\overrightarrow{AF}•\overrightarrow{BC}=(\overrightarrow{AE}+\overrightarrow{EF})•\overrightarrow{BC}$
=$\overrightarrow{AE}•\overrightarrow{BC}+\frac{1}{2}\overrightarrow{DE}•\overrightarrow{BC}$
=$0+\frac{1}{2}|\overrightarrow{DE}||\overrightarrow{BC}|cos\frac{π}{3}$
=$\frac{1}{2}×\frac{1}{2}×1×\frac{1}{2}$
=$\frac{1}{8}$.
故選A.
點評 本題考查向量垂直的充要條件,向量加法的幾何意義,向量的數乘運算,以及向量數量積的運算及計算公式.


 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
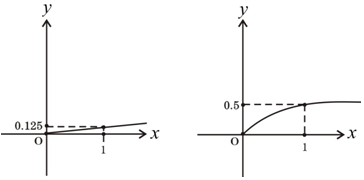
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)=3x-2 | B. | f(x)=3x+2 | C. | f(x)=2x+3 | D. | f(x)=2x-3 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
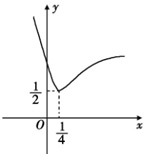 如圖所示的函數F(x)的圖象,由指數函數f(x)=ax與冪函數g(x)=xb“拼接”而成.
如圖所示的函數F(x)的圖象,由指數函數f(x)=ax與冪函數g(x)=xb“拼接”而成.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ?x∈(0,+∞),lnx≠x-2 | B. | ?x∉(0,+∞),lnx=x-2 | ||
| C. | ?x0∈(0,+∞),使lnx0≠x0-2 | D. | ?x0∉(0,+∞),lnx0=x0-2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com