【題目】已知函數(shù)
，其中
．
（Ⅰ）求函數(shù)
的零點個數(shù)；
（Ⅱ）證明： 
是函數(shù)
存在最小值的充分而不必要條件．
【答案】（1）見解析（2）
【解析】試題分析：（Ⅰ）求出函數(shù)
的導數(shù)化簡可得
，對
進行討論可得零點個數(shù)；（Ⅱ）可得
時，無極值；結合（Ⅰ）可得
時， 
的極小值為
，而當
時， 
恒成立，可得極小值即為最小值，故充分性成立，可以舉出反例當
時，必要性不成立.
試題解析：（Ⅰ）由
，得
．
令
，得
，或
．
所以當
時，函數(shù)
有且只有一個零點： 
；當
時，函數(shù)
有兩個相異的零點： 
， 
．
（Ⅱ）① 當
時， 
恒成立，此時函數(shù)
在
上單調遞減，
所以，函數(shù)
無極值．
② 當
時， 
， 
的變化情況如下表：
|
|
|
|
|
|
|
|
|
|
|
|
| ↘ | 極小值 | ↗ | 極大值 | ↘ |
所以， 
時， 
的極小值為
．
又
時， 
，
所以，當
時， 
恒成立．
所以， 
為
的最小值．
故
是函數(shù)
存在最小值的充分條件．
③ 當
時， 
， 
的變化情況如下表：
|
|
|
|
|
|
|
|
|
|
|
|
| ↘ | 極小值 | ↗ | 極大值 | ↘ |
因為當
時， 
，
又
，
所以，當
時，函數(shù)
也存在最小值．
所以， 
不是函數(shù)
存在最小值的必要條件．
綜上， 
是函數(shù)
存在最小值的充分而不必要條件．
高中必刷題系列答案科目：高中數(shù)學 來源： 題型：
【題目】給出40個數(shù)：1,2,4,7,11,16，…，要計算這40個數(shù)的和，如圖給出了該問題的程序框圖，那么框圖①處和執(zhí)行框②處可分別填入（ ）
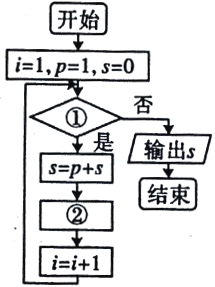
A. 
； 
B. 
； 
C. 
； 
D. 
； 
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f（x）=x2﹣ax﹣2a2（x∈R）．
（1）關于x的不等式f（x）＜0的解集為A，且A[﹣1，2]，求a的取值范圍；
（2）是否存在實數(shù)a，使得當x∈R時， 
成立．若存在給出證明，若不存在說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設集合A={x|x2﹣3x+2=0}，B={x|x2+2（a+1）x+（a2﹣5）=0}．
（1）若A∩B={2}，求實數(shù)a的值；
（2）若A∪B=A，求實數(shù)a的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在幾何體
中，底面
為矩形， 
， 
．點
在棱
上，平面
與棱
交于點
．
（Ⅰ）求證： 
；
（Ⅱ）求證：平面
平面
；
（Ⅲ）若
， 
， 
，平面
平面
，求二面角
的大小．
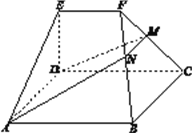
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，四棱錐
的底面是邊長為
的正方形， 
底面
， 
分別為
的中點.
（Ⅰ）求證： 
平面
；
（Ⅱ）若
，試問在線段
上是否存在點
，使得二面角 
的余弦值為
？若存在，確定點
的位置；若不存在，請說明理由.
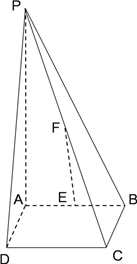
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某奧運會主體育場的簡化鋼結構俯視圖如圖所示，內外兩圈的鋼骨架是離心率相同的橢圓，我們稱這兩個橢圓相似。
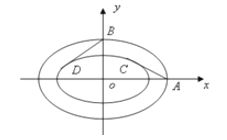
（1）已知橢圓
，寫出與橢圓
相似且焦點在
軸上、短半軸長為
的橢圓
的標準方程；若在橢圓
上存在兩點
、
關于直線
對稱，求實數(shù)
的取值范圍；
（2）從外層橢圓頂點A、B向內層橢圓引切線AC、BD，設內層橢圓方程為
+
=1 (a
b
0)，AC與BD的斜率之積為－
，求橢圓的離心率。
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f（x）=2sin2（ 
+x）+ 
（sin2x﹣cos2x），x∈[ ， 
]．
（1）求 
的值；
（2）求f（x）的單調區(qū)間；
（3）若不等式|f（x）﹣m|＜2恒成立，求實數(shù)m的取值范圍．
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
