
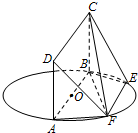
 如圖,AB為圓O的直徑,點E、F在圓O上,AB∥EF,矩形ABCD所在的平面與圓O所在的平面互相垂直.已知AB=2,EF=1.
如圖,AB為圓O的直徑,點E、F在圓O上,AB∥EF,矩形ABCD所在的平面與圓O所在的平面互相垂直.已知AB=2,EF=1.| n1 |
| 3 |
| n2 |
| AF |
| 1 |
| 2 |
| ||
| 2 |
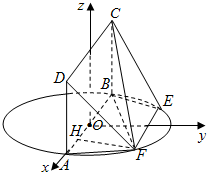 (I)證明:∵平面ABCD⊥平面ABEF,CB⊥AB,平面ABCD∩平面ABEF=AB,
(I)證明:∵平面ABCD⊥平面ABEF,CB⊥AB,平面ABCD∩平面ABEF=AB,| AB-EF |
| 2 |
| 1 |
| 2 |
| AF |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| CD |
| FD |
| 1 |
| 2 |
| ||
| 2 |
| n1 |
| n1 |
| CD |
| n1 |
| FD |
|
| 3 |
| n1 |
| 3 |
| n2 |
| AF |
| 1 |
| 2 |
| ||
| 2 |
| n1 |
| n2 |
| ||||
|
|
| 1 |
| 2 |
| ||
|
| ||
| 4 |
| ||
| 4 |


科目:高中數學 來源: 題型:


查看答案和解析>>
科目:高中數學 來源:2010-2011學年山東省濟南市高三12月質量檢測數學文卷 題型:解答題
(本小題滿分12分)如圖,AB為圓O的直
徑,點E、F在圓O上,AB∥EF,矩形ABCD
所在的平面和圓O所在的平面垂直,且 .
.
⑴求證: ;
;
⑵設FC的中點為M,求證: ;
;
⑶設平面CBF將幾何體分成的兩個錐體的體積分別為 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題


查看答案和解析>>
科目:高中數學 來源:2010年遼寧省錦州市高考數學二模試卷(解析版) 題型:解答題


查看答案和解析>>
科目:高中數學 來源:陜西省寶雞中學2010屆高三適應性訓練(數學理) 題型:填空題
A.(參數方程與極坐標)
直線 與直線
與直線 的夾角大小為
的夾角大小為
 B.(不等式選講)要使關于x的不等式
B.(不等式選講)要使關于x的不等式 在實數
在實數
范圍內有解,則A的取值范圍是
C.(幾何證明選講) 如圖所示,在圓O中,AB是圓O的直
徑AB =8,E為OB.的中點,CD過點E且垂直于AB,
EF⊥AC,則
CF•CA=
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com