在直角坐標系xOy中,設P為兩動圓(x+2)2+y2=(r+2)2,(x-2)2+y2=r2(r>1)的一個交點,記動點P的軌跡為C.給出下列三個結論:
①曲線C過坐標原點;
②曲線C關于x軸對稱;
③設點P(x,y),則有|y|<|2x|.
其中,所有正確的結論序號是 .
【答案】
分析:根據P到兩圓圓心的距離之差是定值,根據雙曲線定義判斷曲線類型,再寫出方程;然后利用方程驗證是否過原點,是否關于x軸對稱,是否滿足|y|<|2x|即可.
解答:解:設A(-2,0),B(2,0),動點P(x,y),
根據題意:|PA|-|PB|=2
∴根據雙曲線的定義判定,P點的軌跡是雙曲線的右支,
方程式:
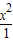
-
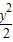
=1,(x>0)
∵(0,0)不是方程的解,∴①不正確;
設點M(x,y)曲線上的任一點,M關于x軸的對稱點為N(x,-y),
∵N的坐標也滿足方程,∴N在曲線上,∴曲線C關于x軸對稱,②正確;
∵4x
2=4(1+
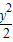
)=4+2y
2>y
2,∴|y|<|2x|.故③正確.
答案是②③
點評:本題借助考查命題的真假判斷,考查雙曲線的定義及定義法求軌跡方程.
定義法求軌跡方程的基本步驟:根據條件判斷動點軌跡類型--根據已知曲線的標準方程求出特征量--寫出軌跡方程,再證明以方程的解為坐標的點都在曲線上.

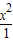 -
-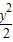 =1,(x>0)
=1,(x>0)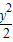 )=4+2y2>y2,∴|y|<|2x|.故③正確.
)=4+2y2>y2,∴|y|<|2x|.故③正確.

 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案 如圖所示,在直角坐標系xOy中,射線OA在第一象限,且與x軸的正半軸成定角60°,動點P在射線OA上運動,動點Q在y軸的正半軸上運動,△POQ的面積為2
如圖所示,在直角坐標系xOy中,射線OA在第一象限,且與x軸的正半軸成定角60°,動點P在射線OA上運動,動點Q在y軸的正半軸上運動,△POQ的面積為2