【題目】已知等邊三角形
的邊長為
，
為
邊的中點，沿
將
折成直二面角
，則三棱錐
的外接球的表面積為_____
【答案】
【解析】
先證明AD⊥平面BCD，利用二面角的定義得知∠BDC＝90°，利用勾股定理可得出△BCD的外接圓直徑為BC，設R為三棱錐A﹣BCD的外接球的半徑，得
，再利用球體表面積公式可得出答案．
如圖所示，
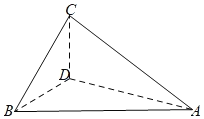
折疊前，由于△ABC時等邊三角形，D為BC的中點，則AD⊥BC，
折疊后，則有AD⊥CD，AD⊥BD，∵BD∩CD＝D，∴AD⊥平面BCD，
∵二面角B﹣AD﹣C為直二面角，∵AD⊥BD，AD⊥CD，則二面角B﹣AD﹣C的平面角為∠BDC＝90°，
且
，
Rt△BCD的外接圓直徑為
，
所以，三棱錐A﹣BCD的外接球半徑為
，
因此，三棱錐A﹣BCD的外接球的表面積為4πR2＝80π．
故答案為：80π
科目：高中數學 來源： 題型：
【題目】以下5條表述中，橫線上填A代表“充分非必要條件”，填B代表“必要非充分條件”，填C代表“充要條件”，填D代表“既非充分也非必要條件”，請將相應的字母填入下列橫線上.
（1）若
，則“
是
與
的等比中項”是“
”的_______.
（2）“數列
為常數列”是“數列既是等差數列又是等比數列”的_______.
（3）若是等比數列，則“
”是“為遞減數列”的_______.
（4）若是公比為
的等比數列，則“
”是“是遞減數列”的_______.
（5）記數列的前
項和為
，則“數列
為遞增數列”是“數列的各項均為大于零”的_______.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2013年華人數學家張益唐證明了孿生素數猜想的一個弱化形式。孿生素數猜想是希爾伯特在1900年提出的23個問題之一，可以這樣描述：存在無窮多個素數p，使得p+2是素數，素數對(p，p+2)稱為孿生素數．在不超過30的素數中，隨機選取兩個不同的數，其中能夠組成孿生素數的概率是
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
.
（1）當
時，試討論方程
的解的個數；
（2）若曲線
和
上分別存在點
，
，使得
是以原點
為直角頂點的直角三角形，且斜邊
的中點在
軸上，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，在四棱柱
中，側棱
底面
，
，
，
，
，
為棱
的中點.
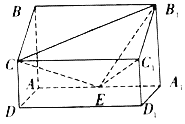
（1）證明：
；
（2）求二面角
的正弦值；
（3）設點
在線段
上，且直線
與平面
所成角的正弦值是
，求線段的長.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
，點
滿足
，記點的軌跡為
.斜率為
的直線
過點
，且與軌跡相交于
兩點.
（1）求軌跡的方程；
（2）求斜率的取值范圍；
（3）在
軸上是否存在定點
，使得無論直線繞點怎樣轉動，總有
成立？如果存在，求出定點；如果不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我國古代著名的
周髀算經
中提到：凡八節二十四氣，氣損益九寸九分六分分之一；冬至晷
長一丈三尺五寸，夏至晷長一尺六寸
意思是：一年有二十四個節氣，每相鄰兩個節氣之間的日影長度差為
分；且“冬至”時日影長度最大，為1350分；“夏至”時日影長度最小，為160分則“立春”時日影長度為
A. 
分B. 
分C. 
分D. 
分
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
