
已知函數 是定義在
是定義在 上的奇函數,給出下列命題:
上的奇函數,給出下列命題:
(1) ;
;
(2)若 在 [0,
在 [0,  上有最小值 -1,則
上有最小值 -1,則 在
在 上有最大值1;
上有最大值1;
(3)若 在 [1,
在 [1,  上為增函數,則
上為增函數,則 在
在  上為減函數;
上為減函數;
(4)若 時,
時, ; 則
; 則 時,
時, 。
。
其中正確的序號是: 。
①②④
解析試題分析:(1)利用奇函數的定義可作出判斷;(2)利用奇函數的定義以及圖象關于原點對稱可作出判斷;(3)利用奇函數在關于原點對稱的區間上單調性一致作出判斷。(4)結合奇函數的對稱性求解得到。
解:(1)因為f(x)是R上的奇函數,所以f(-x)=-f(x),則f(-0)=-f(0),即f(0)=0,故(1)正確;(2)f(x)在[0,+∞)上有最小值-1,即f(x) -1,當x∈(-∞,0)時,-x∈(0,+∞),則f(-x)
-1,當x∈(-∞,0)時,-x∈(0,+∞),則f(-x) -1,所以f(x)=-f(-x)
-1,所以f(x)=-f(-x) 1,即f(x)在(-∞,0)上有最大值1,故(2)正確;(3)因為奇函數的圖象關于原點對稱,所以奇函數在關于原點對稱的區間上單調性一致,故(3)錯誤;(4)若
1,即f(x)在(-∞,0)上有最大值1,故(2)正確;(3)因為奇函數的圖象關于原點對稱,所以奇函數在關于原點對稱的區間上單調性一致,故(3)錯誤;(4)若 時,
時, ; 則根據奇函數,結合對稱性可知,
; 則根據奇函數,結合對稱性可知, 時,
時, 成立,故答案為:①②④.
成立,故答案為:①②④.
考點:函數的性質運用
點評:本題以命題為載體考查函數的奇偶性、單調性,準確把握奇偶函數的定義及其圖象特征是解決本題的基礎


 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:高中數學 來源: 題型:填空題
已知f (x)、g(x)都是定義在R上的函數,如果存在實數m、n使得h (x) =" m" f(x)+ng(x),那么稱h (x)為f (x)、g(x)在R上生成的函數.設 ,
,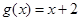 ,若h (x)為f (x)、g(x)在R上生成的一個偶函數,且
,若h (x)為f (x)、g(x)在R上生成的一個偶函數,且 ,則函數h (x)="__________."
,則函數h (x)="__________."
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
設函數 在(0,+∞)上單調遞增,則f (a+1)與f (2)的大小關系是
在(0,+∞)上單調遞增,則f (a+1)與f (2)的大小關系是
| A.f (a+1)= f (2) | B.f (a+1)> f (2) |
| C.f (a+1)< f (2) | D.不確定 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com