
(本小題滿分14分)
如圖8,在直角梯形 中,
中, ,
, ,且
,且 .現以
.現以 為一邊向形外作正方形
為一邊向形外作正方形 ,然后沿邊
,然后沿邊 將正方形
將正方形 翻折,使平面
翻折,使平面 與平面
與平面 互相垂直,如圖9.
互相垂直,如圖9.
(1)求證:平面 平面
平面 ;
;
(2)求平面 與平面
與平面 所成銳二面角的大小.
所成銳二面角的大小.
證明(1)(法一)因為平面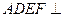 平面
平面 ,
,
且平面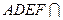 平面
平面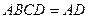 ,
,
又在正方形 中,
中,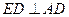 ,
,
所以,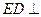 平面
平面 . ………………2分
. ………………2分
而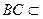 平面
平面 ,
,
所以,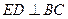 . ………………3分
. ………………3分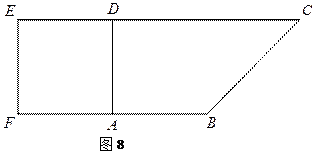
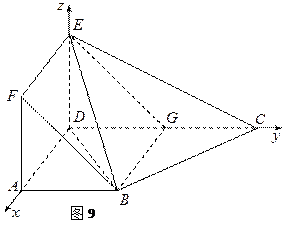
在直角梯形 中,
中, 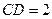 ,
,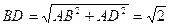 ,
, 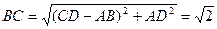 ,
,
所以,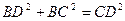 ,
,
所以,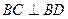 . ………………4分
. ………………4分
又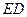 ,
,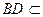 平面
平面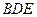 ,
,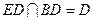 ,
,
所以,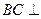 平面
平面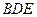 . ………………6分
. ………………6分
而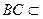 平面
平面 ,
,
所以,平面 平面
平面 . ……………7分
. ……………7分
(法二)同法一,得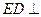 平面
平面 . …………………………2分
. …………………………2分
以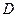 為原點,
為原點,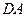 ,
,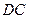 ,
,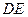 分別為
分別為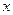 ,
,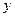
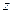 軸,建立空間直角坐標系.
軸,建立空間直角坐標系.
則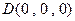 ,
,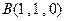 ,
,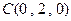 ,
,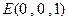 . …………………………3分
. …………………………3分
所以,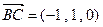 ,
, 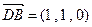 ,
,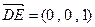 ,
,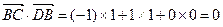 ,
,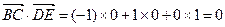 ,
,
所以,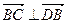 ,
,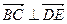 . …………………………………5分
. …………………………………5分
又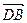 ,
,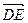 不共線,
不共線,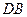 ,
,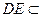 平面
平面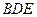 ,
,
所以,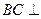 平面
平面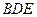 . …………………………6分
. …………………………6分
而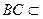 平面
平面 ,
,
所以,平面 平面
平面 . …………………………7分
. …………………………7分
(2)(法一)因為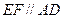 ,
,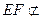 平面
平面 ,
,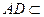 平面
平面 ,
,
所以,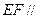 平面
平面 .
.
解析


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案科目:高中數學 來源: 題型:解答題
如圖所示,四棱錐S ABCD的底面是正方形,每條側棱的長都是底面邊長的
ABCD的底面是正方形,每條側棱的長都是底面邊長的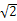 倍,P為側棱SD上的點.
倍,P為側棱SD上的點.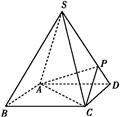
(1)求證:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P AC
AC D的大小;
D的大小;
(3)在(2)的條件下,側棱SC上是否存在一點E,使得BE∥平面PAC?若存在,求SE∶EC的值;若不存在,試說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在棱長為1正方體ABCD-A1B1C1D1中,M和N分別為A1B1和BB1的中點
(1)求直線AM和CN所成角的余弦值;
(2)若P為B1C1的中點,求直線CN與平面MNP所成角的余弦值;
(3)P為B1C1上一點,且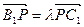 ,當 B1D⊥面PMN時,求
,當 B1D⊥面PMN時,求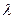 的值.
的值.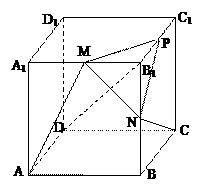
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
已知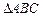 是邊長為2的等邊三角形,
是邊長為2的等邊三角形,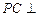 平面
平面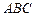 ,
,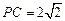 ,
,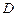 是
是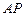 上一動點.
上一動點.
(1)若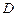 是
是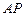 的中點,求直線
的中點,求直線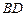 與平面
與平面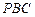 所成的角的正弦值;
所成的角的正弦值;
(2)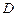 在運動過程中,是否有可能使
在運動過程中,是否有可能使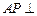 平面
平面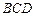 ?請說明理
?請說明理 由.
由.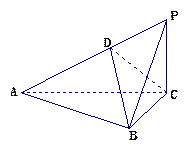
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分15分) 如圖,在三棱錐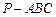 中,
中,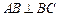 ,
,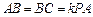 ,點
,點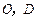 分別是
分別是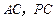 的中點,
的中點,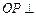 底面
底面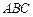 .
.
(1)求證: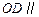 平面
平面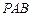 ;
;
(2)當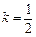 時,求直線
時,求直線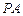 與平面
與平面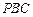 所成角的正弦值;
所成角的正弦值;
(3)當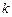 為何值時,
為何值時,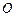 在平面
在平面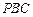 內的射影恰好為
內的射影恰好為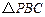 的重心.
的重心.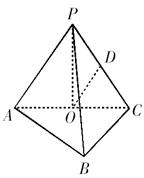
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
四棱錐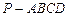 中,底面
中,底面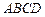 是邊長為2的正方形,
是邊長為2的正方形,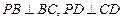 ,且
,且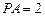 ,點
,點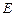 滿足
滿足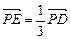 .
.
(1)求證: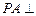 平面
平面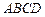 ;
;
(2)求二面角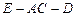 的余弦值;
的余弦值;
(3)在線段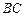 上是否存在點
上是否存在點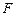 使得
使得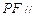 平面
平面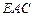 ?若存在,確定點
?若存在,確定點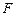 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.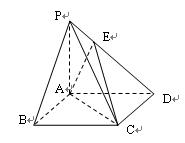
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
已知點(3,1)和(-4,6)在直線 的兩側則
的兩側則 的取值范圍是( )
的取值范圍是( )
| A.a<-7,或 a>24 | B.a=7或 24 | C.-7<a<24 | D.-24<a<7 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com