已知二次函數y=f(x)的圖象經過原點,且f(x-1)=f(x)+x-1.
(1)求f(x)的表達式.
(2)設F(x)=4f(ax)+3a2x-1(a>0且a≠1),當x∈[-1,1]時,F(x)有最大值14,試求a的值.
解:(1)∵函數f(x)圖象經過原點,∴設f(x)=ax
2+bx(a≠0),
∵f(x-1)=f(x)+x-1,
∴a(x-1)
2+b(x-1)=ax
2+bx+x-1,即ax
2-(2a-b)x+a-b=ax
2+(b+1)x-1,
∴
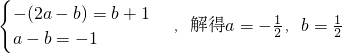
.
∴
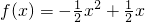
.
(2)由F(x)=4f(a
x)+3a
2x-1(a>0且a≠1),得F(x)=a
2x+2a
x-1,
①當a>1時,令t=a
x,
∵x∈[-1,1],∴
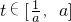
,
∴g(t)=t
2+2t-1=(t+1)
2-2,
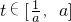
,
∵對稱軸t=-1,∴g(t)在
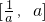
上是增函數.
∴g(a)=a
2+2a-1=14,∴a
2+2a-15=0,解得a=3,a=-5(舍);
②當0<a<1時,
令u=a
x,∵x∈[-1,1],∴
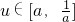
,
∴g(u)=u
2+2u-1=(u+1)
2-2,
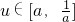
,
∵對稱軸u=-1,∴g(u)在
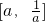
上是增函數.
∴
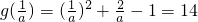
,∴

(舍),∴

,
綜上

或a=3.
分析:(1)待定系數法:由f(x)圖象經過原點可設f(x)=ax
2+bx(a≠0),由f(x-1)=f(x)+x-1得關于a,b的方程組,解出即可;
(2)F(x)可化為F(x)=a
2x+2a
x-1,令t=a
x,則F(x)可轉化為關于t的二次函數,分a>1,0<a<1兩種情況進行討論,利用二次函數的單調性可得最大值,令其為14,可解得a值;
點評:本題考查復合函數的單調性、二次函數的性質,考查分類討論思想,考查學生解決問題的能力.

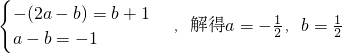 .
.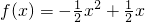 .
.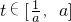 ,
,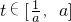 ,
,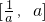 上是增函數.
上是增函數.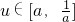 ,
,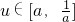 ,
,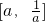 上是增函數.
上是增函數.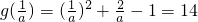 ,∴
,∴ (舍),∴
(舍),∴ ,
, 或a=3.
或a=3.

 已知二次函數y=f(x)的圖象如圖所示:
已知二次函數y=f(x)的圖象如圖所示: