
【題目】如圖所示的幾何體,是將高為2、底面半徑為1的圓柱沿過旋轉軸的平面切開后,將其中一半沿切面向右水平平移后形成的封閉體.![]() 分別為
分別為![]() 的中點,
的中點,![]() 為弧
為弧![]() 的中點,
的中點,![]() 為弧
為弧![]() 的中點.
的中點.
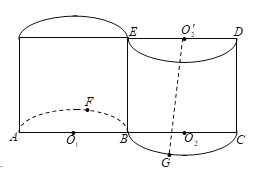
(1)求直線![]() 與底面
與底面![]() 所成的角的大小;
所成的角的大小;
(2)求異面直線![]() 與
與![]() 所成的角的大小(結果用反三角函數值表示).
所成的角的大小(結果用反三角函數值表示).
 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,在五棱錐![]() 中,側面
中,側面![]() 底面
底面![]() ,
,![]() 是邊長為2的正三角形,四邊形
是邊長為2的正三角形,四邊形![]() 為正方形,
為正方形,![]() ,且
,且![]() ,
,![]() 是
是![]() 的重心,
的重心,![]() 是正方形
是正方形![]() 的中心.
的中心.
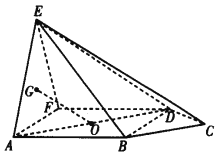
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某網絡平臺從購買該平臺某課程的客戶中,隨機抽取了100位客戶的數據,并將這100個數據按學時數,客戶性別等進行統計,整理得到如表:
學時數 |
|
|
|
|
|
|
|
男性 | 18 | 12 | 9 | 9 | 6 | 4 | 2 |
女性 | 2 | 4 | 8 | 2 | 7 | 13 | 4 |
(1)根據上表估計男性客戶購買該課程學時數的平均值(同一組中的數據用該組區間的中點值作代表,結果保留小數點后兩位);
(2)從這100位客戶中,對購買該課程學時數在20以下的女性客戶按照分層抽樣的方式隨機抽取7人,再從這7人中隨機抽取2人,求這2人購買的學時數都不低于15的概率.
(3)將購買該課程達到25學時及以上者視為“十分愛好該課程者”,25學時以下者視,為“非十分愛好該課程者”.請根據已知條件完成以下![]() 列聯表,并判斷是否有99.9%的把握認為“十分愛好該課程者”與性別有關?
列聯表,并判斷是否有99.9%的把握認為“十分愛好該課程者”與性別有關?
非十分愛好該課程者 | 十分愛好該課程者 | 合計 | |
男性 | |||
女性 | |||
合計 | 100 |
附:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為了組建一支業余足球隊,在高一年級隨機選取50名男生測量身高,發現被測男生的身高全部在![]() 到
到![]() 之間,將測量結果按如下方式分成六組:第1組
之間,將測量結果按如下方式分成六組:第1組![]() ,第2組
,第2組![]() ,…,第6組
,…,第6組![]() ,如圖是按上述分組得到的頻率分布直方圖,以頻率近似概率.
,如圖是按上述分組得到的頻率分布直方圖,以頻率近似概率.
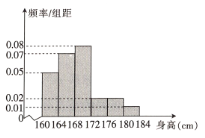
(1)若學校要從中選1名男生擔任足球隊長,求被選取的男生恰好在第5組或第6組的概率;
(2)試估計該校高一年級全體男生身高的平均數(同一組中的數據用該組區間的中點值代表)與中位數;
(3)現在從第5與第6組男生中選取兩名同學擔任守門員,求選取的兩人中最多有1名男生來自第5組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年“雙十一”全網銷售額達![]() 億元,相當于全國人均消費
億元,相當于全國人均消費![]() 元,同比增長
元,同比增長![]() ,監測參與“雙十一”狂歡大促銷的
,監測參與“雙十一”狂歡大促銷的![]() 家電商平臺有天貓、京東、蘇寧易購、網易考拉在內的綜合性平臺,有拼多多等社交電商平臺,有敦煌網、速賣通等出口電商平臺.某大學學生社團在本校
家電商平臺有天貓、京東、蘇寧易購、網易考拉在內的綜合性平臺,有拼多多等社交電商平臺,有敦煌網、速賣通等出口電商平臺.某大學學生社團在本校![]() 名大一學生中采用男女分層抽樣,分別隨機調查了若干個男生和
名大一學生中采用男女分層抽樣,分別隨機調查了若干個男生和![]() 個女生的網購消費情況,制作出男生的頻率分布表、直方圖(部分)和女生的莖葉圖如下:
個女生的網購消費情況,制作出男生的頻率分布表、直方圖(部分)和女生的莖葉圖如下:

男生直方圖
分組(百元) | 男生人數 | 頻率 |
|
|
|
|
|
|
|
|
|
|
| |
|
| |
|
|
|
|
|
|
|
|
|
合計 |
|

女生莖葉圖
(1)請完成頻率分布表的三個空格,并估計該校男生網購金額的中位數(單位:元,精確到個位).
(2)若網購為全國人均消費的三倍以上稱為“剁手黨”,估計該校大一學生中的“剁手黨”人數為多少?從抽樣數據中網購不足![]() 元的同學中隨機抽取
元的同學中隨機抽取![]() 人發放紀念品,則
人發放紀念品,則![]() 人都是女生的概率為多少?
人都是女生的概率為多少?
(3)用頻率估計概率,從全市所有高校大一學生中隨機調查![]() 人,求其中“剁手黨”人數的分布列和期望.
人,求其中“剁手黨”人數的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區不同身高![]() 的未成年男性的體重平均值
的未成年男性的體重平均值![]() 如下表:
如下表:
身高x(cm) | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 |
體重y(kg) | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 | 17.50 | 20.92 | 26.86 | 31.11 |
已知![]() 與
與![]() 之間存在很強的線性相關性,
之間存在很強的線性相關性,
(Ⅰ)據此建立![]() 與
與![]() 之間的回歸方程;
之間的回歸方程;
(Ⅱ)若體重超過相同身高男性體重平均值的![]() 倍為偏胖,低于
倍為偏胖,低于![]() 倍為偏瘦,那么這個地區一名身高
倍為偏瘦,那么這個地區一名身高![]() 體重為
體重為![]()
![]() 的在校男生的體重是否正常?
的在校男生的體重是否正常?
參考數據:![]()
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 中的斜率和截距的最小二乘估計分別為
中的斜率和截距的最小二乘估計分別為
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 的底面
的底面![]() 為直角梯形,
為直角梯形,![]() ,且
,且![]() ,
,![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() 為等邊三角形,
為等邊三角形,![]() 是棱
是棱![]() 上的一點,設
上的一點,設![]() (
(![]() 與
與![]() 不重合).
不重合).
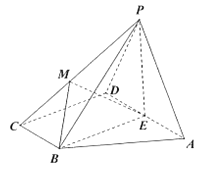
(1)若![]() 平面
平面![]() ,求
,求![]() 的值;
的值;
(2)當![]() 時,求二面角
時,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,兩鐵路線垂直相交于站![]() ,若已知
,若已知![]() 千米,甲火車從
千米,甲火車從![]() 站出發,沿
站出發,沿![]() 方向以
方向以![]() 千米
千米![]() 小時的速度行駛,同時乙火車從
小時的速度行駛,同時乙火車從![]() 站出發,沿
站出發,沿![]() 方向,以
方向,以![]() 千米
千米![]() 小時的速度行駛,至
小時的速度行駛,至![]() 站即停止前行(甲車扔繼續行駛)(兩車的車長忽略不計).
站即停止前行(甲車扔繼續行駛)(兩車的車長忽略不計).
(1)求甲、乙兩車的最近距離(用含![]() 的式子表示);
的式子表示);
(2)若甲、乙兩車開始行駛到甲,乙兩車相距最近時所用時間為![]() 小時,問
小時,問![]() 為何值時
為何值時![]() 最大?
最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com