Question

已知實數x，y滿足約束條件

x≥1 y≤2 x-y≤0

   則z=2x+y的最大值為（　　）

A．3

B．5

C．6

D．不存在

Answer 1

分析：作出不等式組對應的平面區域，利用目標函數的幾何意義，利用數形結合確定z的最大值．

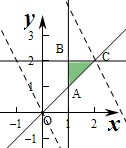
解答：解：作出不等式組對應的平面區域如圖：（陰影部分ABC）．
由z=2x+y得y=-2x+z，
平移直線y=-2x+z，
由圖象可知當直線y=-2x+z經過點C時，直線y=-2x+z的截距最大，
此時z最大．
由

y=2 x-y=0

，解得

x=2 y=2

，即C（2，2）
將C（2，2）的坐標代入目標函數z=2x+y，
得z=2×2+2=6．即z=2x+y的最大值為6．
故選：C．

點評：本題主要考查線性規劃的應用，結合目標函數的幾何意義，利用數形結合的數學思想是解決此類問題的基本方法．