一袋中裝有4n只紅球和n只黑球(所有球的形狀、大小都相同),每一次從袋中摸出兩只球,且每次摸球后均放回袋中.現規定:摸出的兩只球顏色不同則為中獎.設三次摸球恰有一次中獎的概率為P,則當n= 時,使得P最大.
【答案】
分析:根據題意,設某一次中獎的概率為q,由古典概型公式和組合數公式可將q用n表示出來,進而由n次獨立重復試驗恰有k次發生的公式將p用q表示,分析可得q=

時,p最大;
進而可得

=

,解可得n的值,即可得答案.
解答:解:根據題意,設某一次中獎的概率為q,
在4n只紅球和n只黑球任取2只有C
5n2種取法,若摸出的兩只球顏色不同即一紅一黑有C
4n1×C
n1種情況,
則q=

=
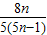
;
若三次摸球恰有一次中獎,
則P=C
31q•(1-q)
2=3q(1-q)
2=

[(2q)(1-q)(1-q)],
分析可得,當2q=1-q,即q=

時,p最大;
若q=

=

,解可得n=5;
即n=5時,p最大;
故答案為5.
點評:本題考查排列、組合的應用,涉及基本不等式的運用,關鍵是熟練應用概率公式,求出兩只球顏色不同的概率以及三次摸球恰有一次中獎的概率.

 時,p最大;
時,p最大; =
= ,解可得n的值,即可得答案.
,解可得n的值,即可得答案. =
=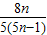 ;
; [(2q)(1-q)(1-q)],
[(2q)(1-q)(1-q)], 時,p最大;
時,p最大; =
= ,解可得n=5;
,解可得n=5;
