
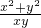 ;②曲線y=f(x)存在與直線x+y+1=0平行的切線.
;②曲線y=f(x)存在與直線x+y+1=0平行的切線. )的曲線y=f(x)的切線的一般式方程;
)的曲線y=f(x)的切線的一般式方程; ,即f(x)=-
,即f(x)=- (x+
(x+ ),
), (1-
(1- ),
), =x+
=x+ ,f′(x)=1-
,f′(x)=1- ,
, ,此方程在D上有解,符合題意.
,此方程在D上有解,符合題意. )的切線切曲線y=f(x)于(x0,x0+
)的切線切曲線y=f(x)于(x0,x0+ ),則切線的斜率為1-
),則切線的斜率為1-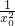 ,
, =(1-
=(1-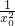 )(x-x0),把點(-1,
)(x-x0),把點(-1, )的坐標代入整理得,
)的坐標代入整理得, -8x0-4=0,解得x0=-
-8x0-4=0,解得x0=- 或x0=2,
或x0=2, 或x0=2分別代入上述方程得所求的切線方程是:y=-
或x0=2分別代入上述方程得所求的切線方程是:y=- x-5和y=
x-5和y= x+1,
x+1, ,當n∈N*時,
,當n∈N*時,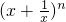 -(xn+
-(xn+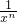 )
) xn-1•
xn-1• +
+ xn-2•
xn-2• +…+
+…+ x2•
x2•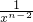 +
+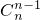 x•
x•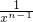
 xn-2+
xn-2+ xn-4+…+
xn-4+…+
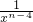 +
+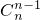
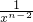 ,
, xn-2+
xn-2+ xn-4+…+
xn-4+…+
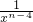 +
+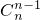
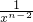
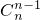
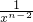 +
+
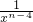 +…+
+…+ xn-4+
xn-4+ xn-2
xn-2 xn-2+
xn-2+ xn-4+…+
xn-4+…+
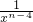 +
+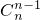
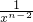

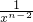 +
+
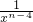 +…+
+…+ xn-4+
xn-4+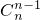 xn-2
xn-2 (xn-2+
(xn-2+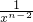 )+
)+ (xn-4+
(xn-4+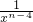 )+…+
)+…+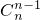 (xn-2+
(xn-2+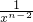 )
) +2
+2 +…+2
+…+2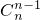 )
) +
+ +…+
+…+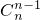 )
) +
+ +
+ +…+
+…+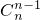 +
+ )-
)- -
- )]
)] ,設過點(-1,
,設過點(-1, )的切線切曲線y=f(x)于(x0,x0+
)的切線切曲線y=f(x)于(x0,x0+ ),則切線的斜率為1-
),則切線的斜率為1-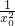 ,于是可求得切線方程,將點(-1,
,于是可求得切線方程,將點(-1, )的坐標代入方程即可求得x0,從而可得過點(-1,
)的坐標代入方程即可求得x0,從而可得過點(-1, )的曲線y=f(x)的切線的一般式方程;
)的曲線y=f(x)的切線的一般式方程; ,當n∈N*時,fn(x)-f(xn)=
,當n∈N*時,fn(x)-f(xn)=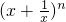 -(xn+
-(xn+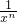 ),利用二項式定理將
),利用二項式定理將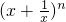 展開,采用倒序相加法可求得2(fn(x)-f(xn)),再利用基本不等式即可證得結論.
展開,采用倒序相加法可求得2(fn(x)-f(xn)),再利用基本不等式即可證得結論.

科目:高中數學 來源: 題型:
| 4+2b-b2 |
| 1-(x-a)2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2+y2 |
| xy |
| 1 |
| 4 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| x2+y2 |
| xy |
| 1 |
| 4 |
查看答案和解析>>
科目:高中數學 來源:《導數及其應用》2013年高三數學一輪復習單元訓練(浙江大學附中)(解析版) 題型:解答題
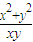 ;②曲線y=f(x)存在與直線x+y+1=0平行的切線.
;②曲線y=f(x)存在與直線x+y+1=0平行的切線. )的曲線y=f(x)的切線的一般式方程;
)的曲線y=f(x)的切線的一般式方程;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com