(1)證明:因為平面
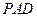
⊥平面

, 平面
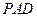
∩平面

=
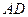
,
又
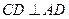
,所以,
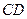
⊥平面
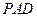
,∴
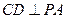
…………6分
又
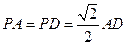
,所以△
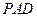
是等腰直角三角形,
且
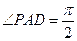
, 即
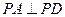
………………7分
又
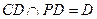
, ∴
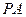
⊥平面
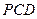
, …………8分
又
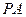
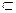
平面
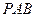
,
所以平面
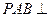
平面
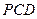
…………………9分
(2)取
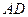
的中點M,連結(jié)
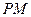
,
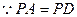
,
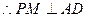
又平面
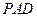
⊥平面

, 平面
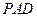
∩平面

=
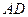
,
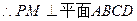
, ……………11分
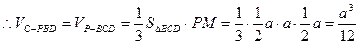
…………14分
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
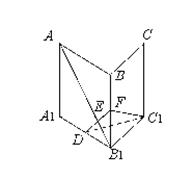
如圖,直三棱柱
ABC—
A1B1C1中,
AC=
BC=1,∠
ACB=90°,
AA1=
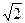
,
D是
A1B1中點.
(1)求證
C1D⊥平面
A1B;
(2)當點
F在
BB1上什么位置時,會使得
AB1⊥平面
C1DF?并證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
在長方體
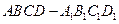
中,點
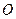
,
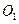
分別是四邊形

,
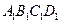
的對角線的交點,點
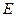
,
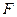
分別是四邊形
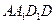
,
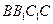
的對角線的交點,點
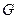
,
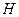
分別是四邊形

,
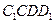
的對角線的交點.求證:
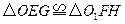
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
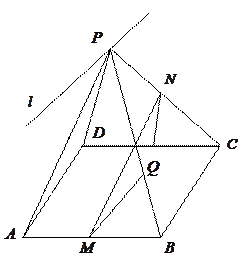
如圖所示,
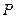
為
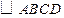
所在平面外一點,
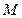
,
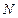
分別是
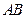
,
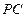
的中點,平面

平面
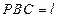
.
(1) 求證:
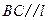
.
(2)
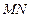
與平面
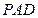
是否平行?試證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
在正方體

中,
E、
F、G、H、M、N分別是正方體六個面的中心.求證:平面
EFG//平面
HMN.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
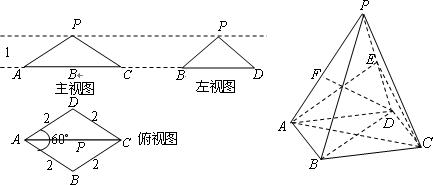
一個四棱錐的三視圖和直觀圖如圖所示,E為側(cè)棱PD的中點.
(1)求證:PB//平面AEC;

(2)若F為側(cè)棱PA上的一點,且
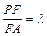
, 則為何值時,PA平面BDF? 并求此時幾何體F—BDC的體積.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知P為△ABC所在平面外一點,G
1、G
2、G
3分別是△PAB、△PCB、△PAC的重心.
(1)求證:平面G
1G
2G
3∥平面ABC;
(2)求S
△
∶S
△ABC.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
對于平面α和直線
m、n,下列命題中真命題是
A.若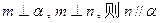 | B.若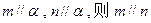 |
C.若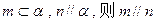 | D.若m//n則m、n與α所成的角相等, |
查看答案和解析>>

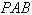 是否垂直于平面
是否垂直于平面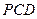 ?
?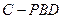 的體積.
的體積.
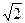 ,
,
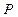
 (2)若F為側(cè)棱PA上的一點,且
(2)若F為側(cè)棱PA上的一點,且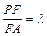 , 則為何值時,PA平面BDF? 并求此時幾何體F—BDC的體積.
, 則為何值時,PA平面BDF? 并求此時幾何體F—BDC的體積.
 ∶S△ABC.
∶S△ABC.