
【題目】在四棱柱![]() 中,底面
中,底面![]() 為矩形,面
為矩形,面![]() ⊥平面
⊥平面![]() ,
,![]() =
=![]() =
=![]() =
=![]() ,
,![]() =2,
=2,![]() 是
是![]() 的中點.
的中點.
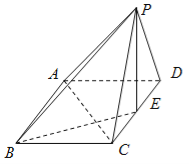
(Ⅰ)求證:![]() ⊥
⊥![]() ;
;
(Ⅱ)求BD與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)見解析(Ⅱ)![]()
【解析】(Ⅰ)∵PD=PC,E為CD的中點,∴PE⊥CD,
∵平面PCD⊥平面ABCD,∴PE⊥平面ABCD,
∴PE⊥AC,(2分)
在Rt△BCE和Rt△ABC中,![]() ,∠ABC=∠BCE=90°,
,∠ABC=∠BCE=90°,
∴Rt△BCE∽Rt△ABC,(4分)
∴∠BAC=∠CBE,∠ACB=∠BEC,
∴∠EBC+∠ACB=∠CAB+∠ACB=90°,
∴BE⊥CA,(5分)
∵BE∩PE=E,
∴AC⊥平面PBE,
∴AC⊥PB;(6分)
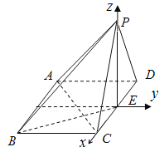
(Ⅱ)以E為坐標原點,如圖建立空間直角坐標系,則P(0,0,1),C(1,0,0),![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,![]() ,(8分)
,(8分)
設平面![]() 的法向量為
的法向量為![]() ,則
,則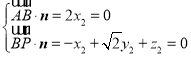 ,取
,取![]() =
=![]() ,則
,則![]() =0,
=0,![]() =-2,∴
=-2,∴![]() =(0,
=(0,![]() ,-2),(10分)
,-2),(10分)
設BD與平面![]() 所成角為
所成角為![]() ,
,
則![]() =
=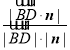 =
=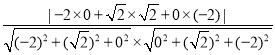 =
=![]() ,(11分)
,(11分)
∴BD與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .(12分)
.(12分)


 全優考典單元檢測卷及歸類總復習系列答案
全優考典單元檢測卷及歸類總復習系列答案 品學雙優卷系列答案
品學雙優卷系列答案科目:高中數學 來源: 題型:
【題目】現階段全國多地空氣質量指數“爆表”.為探究車流量與![]() 濃度是否相關,現對北方某中心城市的車流量最大的地區進行檢測,現采集到
濃度是否相關,現對北方某中心城市的車流量最大的地區進行檢測,現采集到![]() 月某天
月某天![]() 個不同時段車流量與
個不同時段車流量與![]() 濃度的數據,如下表:
濃度的數據,如下表:
車流量 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根據上表中的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)規定當![]() 濃度平均值在
濃度平均值在![]() ,空氣質量等級為優;當
,空氣質量等級為優;當![]() 濃度平均值在
濃度平均值在![]() ,空氣質量等級為良;為使該城市空氣質量為優和良,利用該回歸方程,預測要將車流量控制在每小時多少萬輛內(結果以萬輛做單位,保留整數).
,空氣質量等級為良;為使該城市空氣質量為優和良,利用該回歸方程,預測要將車流量控制在每小時多少萬輛內(結果以萬輛做單位,保留整數).
附:回歸直線方程: ![]() ,其中
,其中 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,函數
,函數![]() .
.
(1)當![]() 時,解不等式
時,解不等式![]() ;
;
(2)若關于![]() 的方程
的方程![]() 的解集中恰好有一個元素,求
的解集中恰好有一個元素,求![]() 的取值范圍;
的取值范圍;
(3)設![]() ,若對任意
,若對任意![]() ,函數
,函數![]() 在區間
在區間![]() 上的最大值與最小值的差不超過1,求
上的最大值與最小值的差不超過1,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{an}滿足a1=1,nan+1=(n+1)an+n(n+1),n∈N* . (Ⅰ)證明:數列{ ![]() }是等差數列;
}是等差數列;
(Ⅱ)設bn=3n ![]() ,求數列{bn}的前n項和Sn .
,求數列{bn}的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學調查了某班全部50名同學參加書法社團和演講社團的情況,數據如下表:(單位:人)
參加書法社團 | 未參加書法社團 | |
參加演講社團 | 8 | 6 |
未參加演講社團 | 6 | 30 |
(I)從該班隨機選1名同學,求該同學至少參加上述一個社團的概率;
(II)在既參加書法社團又參加演講社團的8名同學中,有5名男同學A1,A2,A3,A4,A5,3名女同學B1,B2,B3,現從這5名男同學和3名女同學中各隨機選1人,求A1被選中且B1未被選中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】先后隨機投擲2枚正方體骰子,其中x表示第1枚骰子出現的點數,y表示第2枚骰子出現的點數,
(1)求點P(x,y)在直線y=x﹣1上的概率;
(2)求點P(x,y)滿足y2<4x的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() . 問:是否存在正數m,使得對于任意正數
. 問:是否存在正數m,使得對于任意正數![]() ,可使
,可使![]() 為三角形的三邊構成三角形?如果存在:①試寫出一組x,y,m的值,②求出所有m的值;如果不存在,請說明理由.
為三角形的三邊構成三角形?如果存在:①試寫出一組x,y,m的值,②求出所有m的值;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位有員工1000名,平均每人每年創造利潤10萬元.為了增加企業競爭力,決定優化產業結構,調整出x(x∈N*)名員工從事第三產業,調整后他們平均每人每年創造利潤為10(a﹣ ![]() )萬元(a>0),剩下的員工平均每人每年創造的利潤為原來(1+
)萬元(a>0),剩下的員工平均每人每年創造的利潤為原來(1+ ![]() )倍.
)倍.
(1)若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤,則最多可以整出多少名員工從事第三產業;
(2)若調整出的員工創造的年總利潤始終不高于剩余員工創造的年總利潤,則a的最大取值是多少.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com