
【題目】已知函數f(x)=2x,g(x)=x2+ax(其中a∈R).對于不相等的實數x1,x2,設m=![]() ,n=
,n=![]() ,現有如下命題:
,現有如下命題:
①對于任意不相等的實數x1,x2,都有m>0;
②對于任意的a及任意不相等的實數x1,x2,都有n>0;
③對于任意的a,存在不相等的實數x1,x2,使得m=n;
④對于任意的a,存在不相等的實數x1,x2,使得m=-n.
其中真命題有___________________(寫出所有真命題的序號).
【答案】①④
【解析】對于①,因為f '(x)=2xln2>0恒成立,故①正確
對于②,取a=-8,即g'(x)=2x-8,當x1,x2<4時n<0,②錯誤
對于③,令f '(x)=g'(x),即2xln2=2x+a
記h(x)=2xln2-2x,則h'(x)=2x(ln2)2-2
存在x0∈(0,1),使得h(x0)=0,可知函數h(x)先減后增,有最小值.
因此,對任意的a,m=n不一定成立.③錯誤
對于④,由f '(x)=-g'(x),即2xln2=-2x-a
令h(x)=2xln2+2x,則h'(x)=2x(ln2)2+2>0恒成立,
即h(x)是單調遞增函數,
當x→+∞時,h(x)→+∞
當x→-∞時,h(x)→-∞
因此對任意的a,存在y=a與函數h(x)有交點.④正確


科目:高中數學 來源: 題型:
【題目】已知向量![]() ,
,![]() ,
, ![]()
(1)求函數![]() 的最小正周期及
的最小正周期及![]() 取得最大值時對應的x的值;
取得最大值時對應的x的值;
(2)在銳角三角形ABC中,角A、B、C的對邊為a、b、c,若![]() ,求三角形ABC面積的最大值并說明此時該三角形的形狀.
,求三角形ABC面積的最大值并說明此時該三角形的形狀.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義域為R的函數f(x),若f(x)在(-∞,0)和(0,+∞)上均有零點,則稱函數f(x)為“含界點函數”,則下列四個函數中,不是“含界點函數”的是( )
A. f(x)=x2+bx-1(b∈R) B. f(x)=2-|x-1|
C. f(x)=2x-x2 D. f(x)=x-sin x
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=![]() x3-kx,其中實數k為常數.
x3-kx,其中實數k為常數.
(1)當k=4時,求函數的單調區間;
(2)若曲線y=f(x)與直線y=k只有一個交點,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() .
.
(1)若函數![]() 在
在![]() 上單調遞增,求
上單調遞增,求![]() 的取值范圍;
的取值范圍;
(2)設函數![]() ,若對任意的
,若對任意的![]() ,都有
,都有![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)設![]() ,點
,點![]() 是函數
是函數![]() 與
與![]() 的一個交點,且函數
的一個交點,且函數![]() 與
與![]() 在點
在點![]() 處的切線互相垂直,求證:存在唯一的
處的切線互相垂直,求證:存在唯一的![]() 滿足題意,且
滿足題意,且![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據統計,目前微信用戶已達10億,2016年,諸多傳統企業大佬紛紛嘗試進入微商渠道,讓這個行業不斷地走向正規化、規范化.2017年3月25日,第五屆中國微商博覽會在山東濟南舜耕國際會展中心召開,力爭為中國微商產業轉型升級,某品牌飲料公司對微商銷售情況進行中期調研,從某地區隨機抽取6家微商一周的銷售金額(單位:百元)的莖葉圖如圖所示,其中莖為十位數,葉為個位數.

(1)若銷售金額(單位:萬元)不低于平均值![]() 的微商定義為優秀微商,其余為非優秀微商,根據莖葉圖推斷該地區110家微商中有幾家優秀?
的微商定義為優秀微商,其余為非優秀微商,根據莖葉圖推斷該地區110家微商中有幾家優秀?
(2)從隨機抽取的6家微商中再任取2家舉行消費者回訪調查活動,求恰有1家是優秀微商的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 的定義域為
的定義域為![]() ,如果存在正實數
,如果存在正實數![]() ,使得對任意
,使得對任意![]() ,都有
,都有![]() ,且
,且![]() 恒成立,則稱函數
恒成立,則稱函數![]() 為
為![]() 上的“
上的“![]() 的型增函數”,已知
的型增函數”,已知![]() 是定義在
是定義在![]() 上的奇函數,且在
上的奇函數,且在![]() 時,
時, ![]() ,若
,若![]() 為
為![]() 上的“2017的型增函數”,則實數
上的“2017的型增函數”,則實數![]() 的取值范圍是__________.
的取值范圍是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
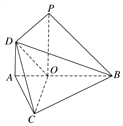
【題目】如圖,在△ABC中,∠ABC=45°,點O在AB上,且OB=OC=![]() AB,PO⊥平面ABC,DA∥PO,DA=AO=
AB,PO⊥平面ABC,DA∥PO,DA=AO=![]() PO.
PO.
(1)求證:PB∥平面COD;
(2)求二面角O-CD-A的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com