高一（1）班參加校生物競賽學生成績的莖葉圖和頻率分布直方圖都受到不同程度的破壞，但可見部分如下，據此解答如下問題：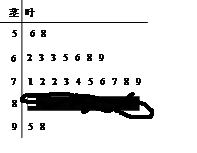
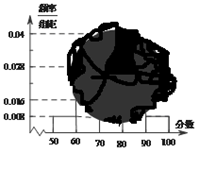
（1）求高一（1）班參加校生物競賽人數及分數在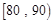
之間的頻數，并計算頻率分布直方圖中 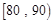間的矩形的高；
（2）若要從分數在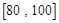
之間的學生中任選兩人進行某項研究，求至少有一人分數在
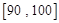之間的概率．
輕松課堂單元期中期末專題沖刺100分系列答案科目：高中數學 來源： 題型：解答題
經銷商經銷某種農產品，在一個銷售季度內，每售出1t該產品獲利潤500元，未售出的產品，每1t虧損300元.根據歷史資料，得到銷售季度內市場需求量的頻率分布直方圖，如右圖所示.經銷商為下一個銷售季度購進了130t該農產品.以x（單位：t，100≤x≤150）表示下一個銷售季度內經銷該農產品的數量，T表示利潤.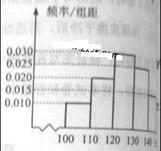
（Ⅰ）將T表示為x的函數
（Ⅱ）根據直方圖估計利潤T不少于57000元的概率;
（Ⅲ）在直方圖的需求量分組中，以各組的區間中點值代表該組的各個值需求量落入該區間的頻率作為需求量取該區間中點值的概率（例如：若x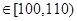
,則取x=105，且x=105的概率等于需求量落入[100，110
，求T的數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
袋中有12個小球，分別為紅球、黑球、黃球、綠球，從中任取一球，得到紅球的概率為
，得到黑球或黃球的概率是
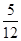，得到黃球或綠球的概率是
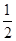，試求得到黑球、黃球、綠球的概率各是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知A，B，C，D，E，F是邊長為1的正六邊形的6個頂點，在頂點取自A，B，C，D，E，F的所有三角形中，隨機(等可能)取一個三角形．設隨機變量X為取出三角形的面積．
(Ⅰ) 求概率P ( X＝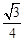
)；
(Ⅱ) 求數學期望E ( X )．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
2012年10月莫言獲得諾貝爾文學獎后，其家鄉山東高密政府準備投資6.7億元打造旅游帶，包括莫言舊居周圍的莫言文化體驗區，紅高粱文化休閑區，愛國主義教育基地等；為此某文化旅游公司向社會公開征集旅游帶建設方案，在收到的方案中甲、乙、丙三個方案引起了專家評委的注意，現已知甲、乙、丙三個方案能被選中的概率分別為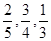
，且假設各自能否被選中是無關的.
（1）求甲、乙、丙三個方案只有兩個被選中的概率；
（2）記甲、乙、丙三個方案被選中的個數為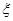
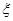，試求的期望.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
市民李生居住在甲地,工作在乙地,他的小孩就讀的小學在丙地,三地之間的道路情況如圖所示.假設工作日不走其它道路,只在圖示的道路中往返,每次在路口選擇道路是隨機的.同一條道路去程與回程是否堵車互不影響.假設李生早上需要先開車送小孩去丙地小學，再返回經甲地趕去乙地上班，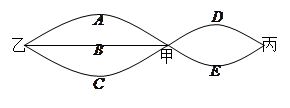
（1）寫出李生可能走的所有路線；（比如DDA表示走D路從甲到丙，再走D路回到甲，然后走A路到達乙）;
（2）假設從丙地到甲地時若選擇走道路D會遇到擁堵，并且從甲地到乙地時若選擇走道路B也會遇到擁堵，其它方向均通暢，但李生不知道相關信息，那么從出發到回到上班地沒有遇到過擁堵的概率是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
甲、乙兩人參加某種選拔測試．在備選的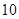
道題中，甲答對其中每道題的概率都是
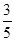，乙能答對其中的
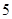道題．規定每次考試都從備選的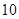道題中隨機抽出
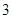道題進行測試，答對一題加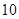分，答錯一題（不答視為答錯）減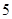分，至少得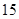
分才能入選．
（1）求甲得分的數學期望；
（2）求甲、乙兩人同時入選的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某校從高二年級學生中隨機抽取60名學生，將其會考的政治成績（均為整數）分成六段：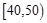 
，
，…，
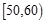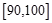后得到如下頻率分布直方圖．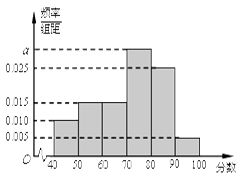
（Ⅰ）求圖中
的值
（Ⅱ）根據頻率分布直方圖，估計該校高二年級學生政治成績的平均分；
（Ⅲ）用分層抽樣的方法在80分以上（含 80分）的學生中抽取一個容量為6的樣本，將該樣本看成一個總體，從中任意選取2人，求其中恰有1人的分數不低于90分的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
設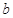
和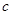
分別是先后拋擲一枚骰子得到的點數，用隨機變量
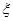表示方程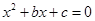
實根的個數（重根按一個計）．
（1）求方程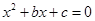有實根的概率；
（2）求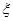的分布列和數學期望；
（3）求在先后兩次出現的點數中有5的條件下，方程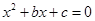有實根的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
分數在
之間的頻數為
，頻率為
，
高一（1）班參加校生物競賽人數為
． 2分
4分
．
6分
人編號為
，
，
，
，
，
，
，
，
，
，
，
，
，
，
. 共
個 
個 10分
11分
12分
