
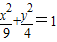 ,則
,則 的取值范圍為 .
的取值范圍為 . 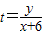 看成是定點A(-6,0)與橢圓
看成是定點A(-6,0)與橢圓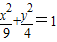 上動點P連線的斜率,且過定點A(-6,0)的直線與橢圓一定有交點,先求出直線與橢圓有交點的特殊情況,即直線與橢圓相切時的t值,其它情況應在兩條切線之間,即可求出范圍.
上動點P連線的斜率,且過定點A(-6,0)的直線與橢圓一定有交點,先求出直線與橢圓有交點的特殊情況,即直線與橢圓相切時的t值,其它情況應在兩條切線之間,即可求出范圍.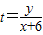 可以斜率,
可以斜率,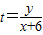 的取值范圍為過定點
的取值范圍為過定點 +
+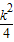 )x2+3k2x+9k2-1=0
)x2+3k2x+9k2-1=0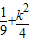 )(9k2-1)=0
)(9k2-1)=0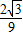 .
.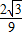 到
到 之間.
之間.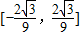
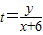 的幾何意義,以及直線與橢圓切線求法,求t范圍做題時應認真分析,找到切入點.
的幾何意義,以及直線與橢圓切線求法,求t范圍做題時應認真分析,找到切入點. 

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com