
【題目】已知函數f(x)=x2+2xsinθ﹣1,x∈[﹣ ![]() ,
, ![]() ].
].
(1)當 ![]() 時,求函數f(x)的最小值;
時,求函數f(x)的最小值;
(2)若函數f(x)在x∈[﹣ ![]() ,
, ![]() ]上是單調增函數,且θ∈[0,2π],求θ的取值范圍.
]上是單調增函數,且θ∈[0,2π],求θ的取值范圍.
【答案】
(1)解:當θ= ![]() 時,f(x)=x2+x﹣1=(x+
時,f(x)=x2+x﹣1=(x+ ![]() )2﹣
)2﹣ ![]() ,
,
由于x∈[﹣ ![]() ,
, ![]() ],故當x=﹣
],故當x=﹣ ![]() 時,f(x)有最小值﹣
時,f(x)有最小值﹣ ![]() ;
;
當x= ![]() 時,f(x)有最大值﹣
時,f(x)有最大值﹣ ![]() .
.
(2)解:因為f(x)=x2+2xsinθ﹣1的對稱軸為x=﹣sinθ,
又欲使f(x)在區間[﹣ ![]() ,
, ![]() ]上是單調函數,
]上是單調函數,
則﹣sinθ≤﹣ ![]() ,或﹣sinθ≥
,或﹣sinθ≥ ![]() ,即sinθ≥
,即sinθ≥ ![]() 或sinθ≤﹣
或sinθ≤﹣ ![]()
因為θ∈[0,2π],
故所求θ的范圍是[ ![]() ,
, ![]() ]∪[
]∪[ ![]() ,
, ![]() ].
].
【解析】(1)當θ= ![]() 時,f(x)=x2+x﹣1=(x+
時,f(x)=x2+x﹣1=(x+ ![]() )2+
)2+ ![]() ,利用二次函數的性質求得f(x)的最大值和最小值.(2)利用f(x)=x2+2xsinθ﹣1的對稱軸為x=﹣sinθ,由題意可得﹣sinθ≤﹣
,利用二次函數的性質求得f(x)的最大值和最小值.(2)利用f(x)=x2+2xsinθ﹣1的對稱軸為x=﹣sinθ,由題意可得﹣sinθ≤﹣ ![]() ,或﹣sinθ≥
,或﹣sinθ≥ ![]() ,求得sinθ的范圍,再結合θ的范圍,確定出θ的具體范圍.
,求得sinθ的范圍,再結合θ的范圍,確定出θ的具體范圍.
【考點精析】關于本題考查的利用導數研究函數的單調性,需要了解一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減才能得出正確答案.
在這個區間單調遞減才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的部分圖象如圖所示,則y=f(x)的圖象可由y=cos2x圖象( )
)的部分圖象如圖所示,則y=f(x)的圖象可由y=cos2x圖象( ) 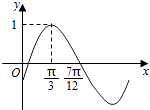
A.向右平移 ![]() 個長度單位
個長度單位
B.向左平移 ![]() 個長度單位
個長度單位
C.向右平移 ![]() 個長度單位
個長度單位
D.向左平移 ![]() 個長度單位
個長度單位
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓W: ![]() ,過原點O作直線l1交橢圓W于A,B兩點,P為橢圓上異于A,B的動點,連接PA,PB,設直線PA,PB的斜率分別為k1 , k2(k1 , k2≠0),過O作直線PA,PB的平行線l2 , l3 , 分別交橢圓W于C,D和E,F.
,過原點O作直線l1交橢圓W于A,B兩點,P為橢圓上異于A,B的動點,連接PA,PB,設直線PA,PB的斜率分別為k1 , k2(k1 , k2≠0),過O作直線PA,PB的平行線l2 , l3 , 分別交橢圓W于C,D和E,F.
(1)若A,B分別為橢圓W的左、右頂點,是否存在點P,使∠APB=90°?說明理由.
(2)求k1k2的值;
(3)求|CD|2+|EF|2的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知指數函數y=g(x)滿足:g(3)=8,定義域為R的函數f(x)= ![]() 是奇函數.
是奇函數.
(1)確定y=g(x),y=f(x)的解析式;
(2)若h(x)=f(x)+a在(﹣1,1)上有零點,求a的取值范圍;
(3)若對任意的t∈(﹣4,4),不等式f(6t﹣3)+f(t2﹣k)<0恒成立,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品特約經銷商根據以往當地的需求情況,得出如圖該種產品日需求量的頻率分布直方圖. 
(1)求圖中a的值,并估計日需求量的眾數;
(2)某日,經銷商購進130件該種產品,根據近期市場行情,當天每售出1件能獲利30元,未售出的部分,每件虧損20元.設當天的需求量為x件(100≤x≤150),純利潤為S元.
(ⅰ)將S表示為x的函數;
(ⅱ)根據直方圖估計當天純利潤S不少于3400元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x+ ![]() 是奇函數.
是奇函數.
(1)若點Q(1,3)在函數f(x)的圖象上,求函數f(x)的解析式;
(2)寫出函數f(x)的單調區間(不要解答過程,只寫結果);
(3)設點A(t,0),B(t+1,0)(t∈R),點P在f(x)的圖象上,且△ABP的面積為2,若這樣的點P恰好有4個,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,圓M的方程為x2+y2﹣8x﹣2y+16=0,若直線kx﹣y+3=0上至少存在一點,使得以該點為圓心,半徑為1的圓與圓M有公共點,則k的取值范圍是( )
A.(﹣∞, ![]() ]
]
B.[0,+∞)
C.[﹣ ![]() ,0]
,0]
D.(﹣∞, ![]() ]∪[0,+∞)
]∪[0,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某電視臺綜藝節目舉辦的挑戰主持人大賽上,七位評委為某選手打出的分數的莖葉統計圖,去掉一個最高分和一個最低分后,所剩數據的平均數和方差分別為( ) 
A.84,4.84
B.84,1.6
C.85,4
D.85,1.6
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com