分析:①由題意可得:BC
1∥AD
1,所以AA
1與BC
1成的角等于AA
1與AD
1成的角.再根據AB=2,側棱
AA1=,可得AA
1與BC
1成不等于45°角.
②由題意可得:線段AB是AA
1與BC
1的公垂線,可得AA
1與BC
1的距離為線段AB的長度.
③連接BC
1,根據題意與二面角平面角的定義可得∠C
1BC是二面角C
1-AB-C的平面角,再利用解三角形的有關知識求出答案.
④連接AD
1,A
1D,由題中條件可得:AD
1與A
1D不垂直,進而得到B
1D與AD
1不垂直,可得B
1D與平面D
1AC不垂直.
解答:解:①由題意可得:ABCD-A
1B
1C
1D
1是正四棱柱,所以BC
1∥AD
1,所以AA
1與BC
1成的角等于AA
1與AD
1成的角.
又因為正方形ABCD的邊長為AB=2,側棱
AA1=,
所以AA
1與BC
1成不等于45°角,所以①錯誤.
②由正四棱柱ABCD-A
1B
1C
1D
1的結構特征可得:線段AB是AA
1與BC
1的公垂線,所以AA
1與BC
1的距離為線段AB的長度,所以AA
1與BC
1的距離為2,所以②正確.
③連接BC
1,由正四棱柱的結構特征可得AB⊥BC
1,AB⊥BC,所以根據二面角平面角的定義可得∠C
1BC是二面角C
1-AB-C的平面角.
因為正方形ABCD的邊長為AB=2,側棱
AA1=,
所以tan∠C
1BC=
=,所以二面角C
1-AB-C為
arctan,所以③正確.
④連接AD
1,A
1D,因為正方形ABCD的邊長為AB=2,側棱
AA1=,所以AD
1與A
1D不垂直,所以根據三垂線定理可得B
1D與AD
1不垂直,所以B
1D與平面D
1AC不垂直,所以④錯誤.
故答案為:②③
點評:此題主要考查線面垂直的判斷定理與異面直線的距離,以及考查線線角與二面角的有關知識,解決異面直線的距離問題的關鍵是找出兩條異面直線的公垂線,而解決空間角的關鍵是找出空間角,其步驟是:作角,證角,求角,此題綜合性較強考查的問題很基礎,屬于中檔題.

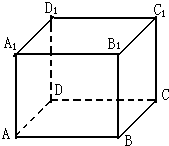 在正四棱柱ABCD-A1B1C1D1中,如果底邊正方形ABCD的邊長為AB=2,側棱AA1=
在正四棱柱ABCD-A1B1C1D1中,如果底邊正方形ABCD的邊長為AB=2,側棱AA1=

 如圖,在正四棱柱ABCD-A1B1C1D1中,棱長AA1=2,AB=1,E是AA1的中點.
如圖,在正四棱柱ABCD-A1B1C1D1中,棱長AA1=2,AB=1,E是AA1的中點. 如圖,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分別為B1B和A1D的中點.
如圖,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分別為B1B和A1D的中點.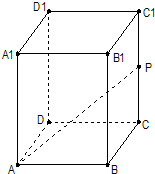 (2012•長寧區一模)在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的邊長為2,點P是CC1的中點,直線AP與平面BCC1B1成30°角,求異面直線BC1和AP所成角的大小.(結果用反三角函數值表示)
(2012•長寧區一模)在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的邊長為2,點P是CC1的中點,直線AP與平面BCC1B1成30°角,求異面直線BC1和AP所成角的大小.(結果用反三角函數值表示)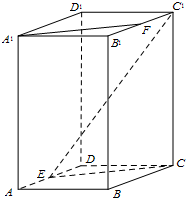 (2012•昌平區二模)在正四棱柱ABCD-A1B1C1D1中,E為AD中點,F為B1C1中點.
(2012•昌平區二模)在正四棱柱ABCD-A1B1C1D1中,E為AD中點,F為B1C1中點.