
| A. | 16 | B. | 12 | C. | 10 | D. | 8 |
分析 作PH∥CD,交AD于H,過H作HF∥AB,交BD于F,過FE∥CD,交BC于E,連結PE,則四邊形PEFH是過P作四面體的截面,且截面平行于直線AB和CD,由AP=2PC,三棱錐A-BCD的所有棱長均為6,能求出該截面的周長.
解答 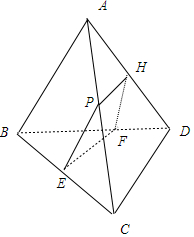 解:∵三棱錐A-BCD的所有棱長均為6,點P在AC上,
解:∵三棱錐A-BCD的所有棱長均為6,點P在AC上,
且AP=2PC,過P作四面體的截面,使截面平行于直線AB和CD,
作PH∥CD,交AD于H,過H作HF∥AB,交BD于F,過FE∥CD,
交BC于E,連結PE,
則四邊形PEFH是過P作四面體的截面,且截面平行于直線AB和CD,
∵AP=2PC,三棱錐A-BCD的所有棱長均為6,
∴PH=EF=$\frac{2}{3}×6=4$,HF=PE=$\frac{1}{3}×6=2$,
∴該截面PEFH的周長為:4+4+2+2=12.
故選:B.
點評 本題考查截面的周長的求法,是中檔題,解題時要認真審題,注意空間培養.


科目:高中數學 來源: 題型:選擇題
| A. | $6\sqrt{2}$ | B. | $3+3\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{{\sqrt{2016}}}$ | B. | $\frac{1}{{\sqrt{2017}}}$ | C. | $\frac{1}{{\sqrt{2018}}}$ | D. | $\frac{1}{{\sqrt{2019}}}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
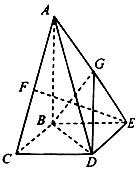 如圖所示,在四棱錐A-BCDE中,AB⊥平面BCDE,四邊形BCDE為矩形,F為AC的中點,AB=BC=2,BE=$\sqrt{2}$.
如圖所示,在四棱錐A-BCDE中,AB⊥平面BCDE,四邊形BCDE為矩形,F為AC的中點,AB=BC=2,BE=$\sqrt{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|x>2} | B. | {x|0≤x<2} | C. | {x|0<x≤2} | D. | {x|x≤2} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
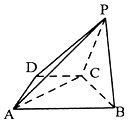 如圖,已知四棱錐P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.
如圖,已知四棱錐P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com