
(本小題滿分14分)
如圖所示,在一個特定時段內,以點E為中心的10海里以內海域被設為警戒水域.點E正北40 海里處有一個雷達觀測站A,某時刻測得一艘勻速直線行駛的船只位于點A北偏東30°且與點A相距100海里的位置B,經過2小時又測得該船已行駛到點A北偏東60°且與點A相距20
海里處有一個雷達觀測站A,某時刻測得一艘勻速直線行駛的船只位于點A北偏東30°且與點A相距100海里的位置B,經過2小時又測得該船已行駛到點A北偏東60°且與點A相距20 海里的位置C.
海里的位置C.
(1)求該船的行駛速度(單位:海里/小時);
(2)若該船不改變航行方向繼續行駛.判斷它是否會進入警戒水域,并說明理由.
(1)10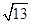 ;(2)該船行駛的速度為10
;(2)該船行駛的速度為10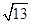 海里/小時,若該船不改變航行方向則會進入警戒水域
海里/小時,若該船不改變航行方向則會進入警戒水域
解析試題分析:(1)如圖建立平面直角坐標系:設一個單位為10海里
則坐標平面中AB = 10,AC = 2 A(0,0),E(0, -4
A(0,0),E(0, -4 )
)
再由方位角可求得:B(5,5 ),C(3,
),C(3, )………………4分
)………………4分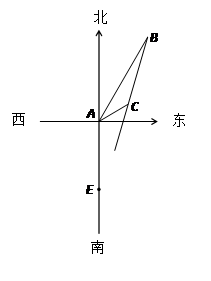
所以|BC| = 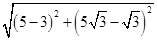 = 2
= 2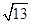
……………6分
所以BC兩地的距離為20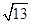 海里
海里
所以該船行駛的速度為10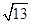 海里/小時
海里/小時
………………7分
(2)直線BC的斜率為 = 2
= 2
所以直線BC的方程為:y- = 2
= 2 (x-3)
(x-3)
即2 x-y-5
x-y-5 =0………10分
=0………10分
所以E點到直線BC的距離為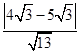 =
= 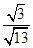 < 1………12分
< 1………12分
所以直線BC會與以E為圓心,以一個單位長為半徑的圓相交,
所以若該船不改變航行方向則會進入警戒水域。……………14分
答:該船行駛的速度為10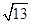 海里/小時,若該船不改變航行方向則會進入警戒水域。
海里/小時,若該船不改變航行方向則會進入警戒水域。
考點:本題考查了直線與圓的實際運用
點評:解直線與圓的問題,要盡量充分地利用平面幾何中圓的性質,利用幾何法解題要比解析方法來得簡捷


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
港口A北偏東30°方向的C處有一檢查站,港口正東方向的B處有一輪船,距離檢查站為31海里,該輪船從B處沿正西方向航行20海里后到達D處觀測站,已知觀測站與檢查站距離21海里,問檢查站C離港口A有多遠?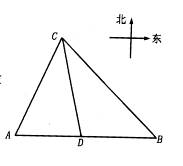
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某興趣小組測量電視塔AE的高度H(單位:m),如示意圖,垂直放置的標桿BC的高度h=4m,仰角∠ABE= ,∠ADE=
,∠ADE= 。
。
(1) 該小組已經測得一組 、
、 的值,tan
的值,tan =1.24,tan
=1.24,tan =1.20,請據此算出H的值;
=1.20,請據此算出H的值;
(2) 該小組分析若干測得的數據后,認為適當調整標桿到電視塔的距離d(單位:m),使 與
與 之差較大,可以提高測量精確度。若電視塔的實際高度為125m,試問d為多少時,
之差較大,可以提高測量精確度。若電視塔的實際高度為125m,試問d為多少時,

 最大?
最大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
本題滿分10分)
一艘輪船按照北偏西50°的方向,以15海里每小時的速度航行,一個燈塔M原來在輪船的北偏東10°方向上,經過40分鐘,輪船與燈塔的距離是 海里,則燈塔和輪船原來的距離為多少?
海里,則燈塔和輪船原來的距離為多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com