
【題目】已知二階矩陣M有特征值λ=8及對應的一個特征向量 ![]() =[
=[ ![]() ],并且矩陣M對應的變換將點(﹣1,2)變換成(﹣2,4).
],并且矩陣M對應的變換將點(﹣1,2)變換成(﹣2,4).
(1)求矩陣M;
(2)求矩陣M的另一個特征值.
【答案】
(1)解:設矩陣A= ![]() ,這里a,b,c,d∈R,
,這里a,b,c,d∈R,
則 ![]()
![]() =8
=8 ![]() =
= ![]() ,
,
故 ![]() ,
,
由于矩陣M對應的變換將點(﹣1,2)換成(﹣2,4).
則 ![]()
![]() =
= ![]() ,
,
故 ![]()
聯立以上兩方程組解得a=6,b=2,c=4,d=4,故M= ![]()
(2)解:由(1)知,矩陣M的特征多項式為f(λ)=(λ﹣6)(λ﹣4)﹣8=λ2﹣10λ+16,
故矩陣M的另一個特征值為2
【解析】(1)先設矩陣A= ![]() ,這里a,b,c,d∈R,由二階矩陣M有特征值λ=8及對應的一個特征向量e1及矩陣M對應的變換將點(﹣1,2)換成(﹣2,4).得到關于a,b,c,d的方程組,即可求得矩陣M;(2)由(1)知,矩陣M的特征多項式為f(λ)=(λ﹣6)(λ﹣4)﹣8=λ2﹣10λ+16,從而求得另一個特征值為2.
,這里a,b,c,d∈R,由二階矩陣M有特征值λ=8及對應的一個特征向量e1及矩陣M對應的變換將點(﹣1,2)換成(﹣2,4).得到關于a,b,c,d的方程組,即可求得矩陣M;(2)由(1)知,矩陣M的特征多項式為f(λ)=(λ﹣6)(λ﹣4)﹣8=λ2﹣10λ+16,從而求得另一個特征值為2.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】一個盒子中裝有1個紅球和2個白球,這3個球除顏色外完全相同,有放回地連續抽取2次,每次從中任意抽取出1個球,則:
(1)第一次取出白球,第二次取出紅球的概率;
(2)取出的2個球是1紅1白的概率;
(3)取出的2個球中至少有1個白球的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場舉行有獎促銷活動,顧客購買一定金額的商品后即可抽獎.抽獎方法是:從裝有![]() 個紅球
個紅球![]() ,
,![]() 和
和![]() 個白球
個白球![]() 的甲箱與裝有
的甲箱與裝有![]() 個紅球
個紅球![]() ,
,![]() 和
和![]() 個白球
個白球![]() ,
,![]() 的乙箱中,各隨機摸出
的乙箱中,各隨機摸出![]() 個球,若模出的
個球,若模出的![]() 個球都是紅球則中獎,否則不中獎.
個球都是紅球則中獎,否則不中獎.
(1)用球的標號列出所有可能的模出結果;
(2)有人認為:兩個箱子中的紅球比白球多所以中獎的概率大于不中獎的概率,你認為正確嗎?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在四棱錐![]() 中,四邊形
中,四邊形![]() 為矩形,
為矩形, ![]() 為等腰三角形,
為等腰三角形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() 的中點.
的中點.
(1)證明: ![]() 平面
平面![]() ;
;
(2)證明:平面![]() 平面
平面![]() ;
;
(3)求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,某市實驗中學校領導審時度勢,深化教育教學改革,經過師生共同努力,高考成績碩果累累,捷報頻傳,尤其是2017年某著名高校在全國范圍內錄取的大學生中就有25名來自該中學.下表為該中學近5年被錄取到該著名高校的學生人數.(記2013年的年份序號為1,2014年的年份序號為2,依此類推……)
年份序號 | 1 | 2 | 3 | 4 | 5 |
錄取人數 | 10 | 13 | 17 | 20 | 25 |
(1)求![]() 關于
關于![]() 的線性回歸方程,并估計2018年該中學被該著名高校錄取的學生人數(精確到整數);
的線性回歸方程,并估計2018年該中學被該著名高校錄取的學生人數(精確到整數);
(2)若在第1年和第4年錄取的大學生中按分層抽樣法抽取6人,再從這6人中任選2人,求這2人中恰好有一位來自第1年的概率.
參考數據:![]() ,
,![]() .
.
參考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
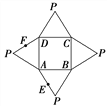
【題目】如圖是一幾何體的平面展開圖,其中ABCD為正方形,E,F分別為PA,PD的中點,
在此幾何體中,給出下面四個結論:
①直線BE與直線CF異面; ②直線BE與直線AF異面;
③直線EF∥平面PBC; ④平面BCE⊥平面PAD.
其中正確的有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某基地蔬菜大棚采用水培、無土栽培方式種植各類蔬菜.過去50周的資料顯示,該地周光照量![]() (小時)都在30小時以上,其中不足50小時的周數有5周,不低于50小時且不超過70小時的周數有35周,超過70小時的周數有10周.根據統計,該基地的西紅柿增加量
(小時)都在30小時以上,其中不足50小時的周數有5周,不低于50小時且不超過70小時的周數有35周,超過70小時的周數有10周.根據統計,該基地的西紅柿增加量![]() (百斤)與使用某種液體肥料
(百斤)與使用某種液體肥料![]() (千克)之間對應數據為如圖所示的折線圖.
(千克)之間對應數據為如圖所示的折線圖.

(1)依據數據的折線圖,是否可用線性回歸模型擬合![]() 與
與![]() 的關系?請計算相關系數
的關系?請計算相關系數![]() 并加以說明(精確到0.01).(若
并加以說明(精確到0.01).(若![]() ,則線性相關程度很高,可用線性回歸模型擬合)
,則線性相關程度很高,可用線性回歸模型擬合)
(2)蔬菜大棚對光照要求較大,某光照控制儀商家為該基地提供了部分光照控制儀,但每周光照控制儀最多可運行臺數受周光照量![]() 限制,并有如下關系:
限制,并有如下關系:
周光照量 |
|
|
|
光照控制儀最多可運行臺數 | 3 | 2 | 1 |
若某臺光照控制儀運行,則該臺光照控制儀周利潤為3000元;若某臺光照控制儀未運行,則該臺光照控制儀周虧損1000元.若商家安裝了3臺光照控制儀,求商家在過去50周周總利潤的平均值.
附:相關系數公式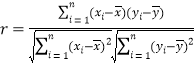 ,參考數據
,參考數據![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的上頂點到右頂點的距離為
)的上頂點到右頂點的距離為![]() ,左焦點為
,左焦點為![]() ,過點
,過點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() ,
, ![]() 兩點.
兩點.
(Ⅰ)求橢圓![]() 的標準方程及
的標準方程及![]() 的取值范圍;
的取值范圍;
(Ⅱ)在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使
,使![]() 恒為定值?若存在,求出點
恒為定值?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com