
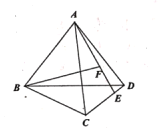
【題目】如圖,已知正四面體![]() 的棱長為2,
的棱長為2,![]() 是棱
是棱![]() 上一動點,若
上一動點,若![]() 于
于![]() ,則線段
,則線段![]() 的長度的最小值是______
的長度的最小值是______
【答案】![]()
【解析】
取![]() 的中點為
的中點為![]() ,取
,取![]() 的中點為
的中點為![]() ,連接
,連接![]() ,在
,在![]() 上取一點
上取一點![]() ,使得
,使得![]() ,取
,取![]() 的中點為
的中點為![]() ,連接
,連接![]() ,則
,則![]() 平面
平面![]() ,則點
,則點![]() 在以點
在以點![]() 為球心、
為球心、![]() 為直徑的球面上,且軌跡是以點
為直徑的球面上,且軌跡是以點![]() 為圓心的一段圓弧,結合幾何知識即可求出答案.
為圓心的一段圓弧,結合幾何知識即可求出答案.
解:∵![]() ,
,
∴點![]() 在以
在以![]() 為直徑的球面上,取
為直徑的球面上,取![]() 的中點為
的中點為![]() ,
,
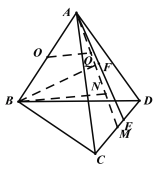
∵點![]() 在
在![]() 中,
中,
由于一個平面截一個球所得的是一個圓面,
∴點![]() 的軌跡為一段圓弧,
的軌跡為一段圓弧,
取![]() 的中點為
的中點為![]() ,連接
,連接![]() ,在
,在![]() 上取一點
上取一點![]() ,使得
,使得![]() ,
,
在等邊![]() 中,易得點
中,易得點![]() 為
為![]() 的中心,
的中心,
∴在正四面體![]() 中,易得
中,易得![]() 平面
平面![]() ,
,
取![]() 的中點為
的中點為![]() ,連接
,連接![]() ,則
,則![]() ,則
,則![]() 平面
平面![]() ,
,
由于一個平面截一個球所得的是一個圓面,且球心與這個圓的圓心所在直線與該平面垂直,
∴點![]() 的軌跡是以點
的軌跡是以點![]() 為圓心的一段圓弧,
為圓心的一段圓弧,
又![]() ,∴球
,∴球![]() 的半徑為
的半徑為![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,則
,則![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴圓![]() 的半徑
的半徑![]() ,
,
而![]() ,
,
∴![]() ,
,
故答案為:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知
中,已知![]() 、
、![]() 分別為橢圓
分別為橢圓![]() 的左、右焦點,直線
的左、右焦點,直線![]() 過點
過點![]() 且垂直于橢圓的長軸,動直線
且垂直于橢圓的長軸,動直線![]() 垂直于直線
垂直于直線![]() 于點
于點![]() ,線段
,線段![]() 的中垂線交
的中垂線交![]() 于點
于點![]() .記點
.記點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程,并說明
的方程,并說明![]() 是什么曲線;
是什么曲線;
(2)若直線![]() 與曲線
與曲線![]() 交于兩點
交于兩點![]() 、
、![]() ,則在圓
,則在圓![]() 上是否存在兩點
上是否存在兩點![]() 、
、![]() ,使得
,使得![]() ,
,![]() ?若存在,請求出
?若存在,請求出![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 長軸長為4,右焦點
長軸長為4,右焦點![]() 到左頂點的距離為3.
到左頂點的距離為3.
(1)求橢圓![]() 的方程;
的方程;
(2)設過原點![]() 的直線交橢圓于
的直線交橢圓于![]() 兩點(
兩點(![]() 不在坐標軸上),連接
不在坐標軸上),連接![]() 并延長交橢圓于點
并延長交橢圓于點![]() ,若
,若![]() ,求四邊形
,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“雜交水稻之父”袁隆平一生致力于雜交水稻技術的研究、應用與推廣,發明了“三系法”秈型雜交水稻,成功研究出“兩系法”雜交水稻,創建了超級雜交稻技術體系,為我國糧食安全、農業科學發展和世界糧食供給做出了杰出貢獻;某雜交水稻種植研究所調查某地水稻的株高,得出株高(單位:cm)服從正態分布,其密度曲線函數為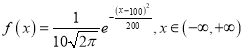 ,則下列說法正確的是( )
,則下列說法正確的是( )
A.該地水稻的平均株高為100cm
B.該地水稻株高的方差為10
C.隨機測量一株水稻,其株高在120cm以上的概率比株高在70cm以下的概率大
D.隨機測量一株水稻,其株高在(80,90)和在(100,110)(單位:cm)的概率一樣大
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在創建“全國衛生文明城”的過程中,環保部門對某市市民進行了一次垃圾分類知識的網絡問卷調查,每一位市民僅有一次參加機會,通過隨機抽樣,得到參加問卷調查的1000人的得分(滿分:100分)數據,統計結果如下表所示.
組別 |
|
|
|
|
|
|
|
頻數 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(Ⅰ)已知此次問卷調查的得分![]() 服從正態分布
服從正態分布![]() ,
,![]() 近似為這1000人得分的平均值(同一組中的數據用該組區間的中點值為代表),請利用正態分布的知識求
近似為這1000人得分的平均值(同一組中的數據用該組區間的中點值為代表),請利用正態分布的知識求![]() ;
;
(Ⅱ)在(Ⅰ)的條件下,環保部門為此次參加問卷調查的市民制定如下獎勵方案:
(i)得分不低于![]() 的可以獲贈2次隨機話費,得分低于
的可以獲贈2次隨機話費,得分低于![]() 的可以獲贈1次隨機話費;
的可以獲贈1次隨機話費;
(ii)每次贈送的隨機話費和相應的概率如下表.現市民甲要參加此次問卷調查,記![]() 為該市民參加問卷調查獲贈的話費,求
為該市民參加問卷調查獲贈的話費,求![]() 的分布列及數學期望.
的分布列及數學期望.
贈送的隨機話費(單位:元) | 20 | 40 |
概率 |
|
|
附:若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《算法統宗》是中國古代數學名著,由明代數學家程大位編著,它對我國民間普及珠算和數學知識起到了很大的作用,是東方古代數學的名著.在這部著作中,許多數學問題都是以歌訣形式呈現的,“九兒問甲歌”就是其中一首:“一個公公九個兒,若問生年總不知,自長排來差三歲,共年二百又零七,借問長兒多少歲,各兒歲數要詳推.”這首歌決的大意是:“一位老公公有九個兒子,九個兒子從大到小排列,相鄰兩人的年齡差三歲,并且兒子們的年齡之和為207歲,請問大兒子多少歲,其他幾個兒子年齡如何推算.”在這個問題中,記這位公公的第![]() 個兒子的年齡為
個兒子的年齡為![]() ,則
,則![]() ( )
( )
A.17B.29C.23D.35
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com