分析:(1)利用勾股定理的逆定理可得AC⊥BC.利用線面垂直的性質定理可得CC
1⊥AC,再利用線面垂直的判定定理即可證明結論;
(2)利用直三棱柱的性質、正方形的性質、三角形的中位線定理即可得出ED∥AC
1,再利用線面平行的判定定理即可證明結論;
(3)取BC的中點M,連接DM,利用三角形的中位線定理可得
DMAC,再利用線面垂直的性質定理可得DM⊥平面BCC
1B
1.利用三棱錐的體積計算公式即可得出.
解答:(1)證明:∵底面三邊長AC=3,BC=4,AB=5.
∴AB
2=AC
2+BC
2,∴∠ACB=90°,∴AC⊥BC.
∵CC
1⊥平面ABC,AC?平面ABC.
∴AC⊥CC
1.
又BC∩CC
1=C,∴AC⊥平面BCC
1B
1,
BC
1?平面BCC
1B
1,
∴AC⊥BC
1.
(2)證明:設CB
1∩BC
1=E,連接ED.
由正方形BCC
1B
1可得E為BC
1的中點,又D為AB的中點,∴AC
1∥ED.
∵ED?平面CDB
1,AC
1?平面CDB
1,
∴AC
1∥平面CDB
1.
(3)解:取BC的中點M,連接DM,則
DMAC,
∵AC⊥平面BCC
1B
1,∴DM⊥平面BCC
1B
1.
∴
VC1-CDB1=VD-CB1C1=
S△CB1C1×DM=
××4×4×=4.
點評:熟練掌握勾股定理的逆定理、線面垂直的判定和性質定理、直三棱柱的性質、正方形的性質、三角形的中位線定理、線面平行的判定定理、三棱錐的體積計算公式是解題的關鍵.

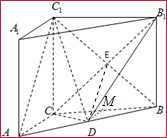
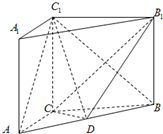 如圖,在三棱柱ABC=A1B1C1中,AC=3,CC1⊥平面ABC,BC=4,AB=5,AA1=4,點D是AB的中點.
如圖,在三棱柱ABC=A1B1C1中,AC=3,CC1⊥平面ABC,BC=4,AB=5,AA1=4,點D是AB的中點.


 如圖,在三棱柱ABC-A'B'C'中,若E、F分別為AB、AC的中點,平面EB'C'F將三棱柱分成體積為V1、V2的兩部分,那么V1:V2為( )
如圖,在三棱柱ABC-A'B'C'中,若E、F分別為AB、AC的中點,平面EB'C'F將三棱柱分成體積為V1、V2的兩部分,那么V1:V2為( ) 如圖,在三棱柱ABC-A1B1C1中,四邊形A1ABB1為菱形,∠A1AB=60°,四邊形BCC1B1為矩形,若AB⊥BC且AB=4,BC=3
如圖,在三棱柱ABC-A1B1C1中,四邊形A1ABB1為菱形,∠A1AB=60°,四邊形BCC1B1為矩形,若AB⊥BC且AB=4,BC=3 (2013•通州區一模)如圖,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2
(2013•通州區一模)如圖,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2 如圖,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分別在線段B1C1上,B1E=3EC1,AC=BC=CC1=4.
如圖,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分別在線段B1C1上,B1E=3EC1,AC=BC=CC1=4.