
【題目】已知拋物線C:![]() 的焦點為F,直線l過點
的焦點為F,直線l過點![]() ,交拋物線于A、B兩點.
,交拋物線于A、B兩點.
(1)若P為![]() 中點,求l的方程;
中點,求l的方程;
(2)求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)方法一:利用點差法求中點弦所在直線斜率,再根據點斜式得結果;注意驗證所求直線與拋物線有兩個交點;
方法二:設中點弦所在直線方程,與拋物線方程聯立,利用韋達定理以及中點坐標公式求中點弦所在直線斜率,再根據點斜式得結果;注意考慮中點弦直線斜率不存在的情況是否滿足題意;
(2)由拋物線的定義轉化![]() ,方法一:設直線l:
,方法一:設直線l:![]() ,與拋物線方程聯立,利用韋達定理以及二次函數性質求最值,注意比較直線斜率不存在的情況
,與拋物線方程聯立,利用韋達定理以及二次函數性質求最值,注意比較直線斜率不存在的情況![]() 的值;方法二:設直線l:
的值;方法二:設直線l:![]() ,與拋物線方程聯立,利用韋達定理以及二次函數性質求最值,此種設法已包含直線斜率不存在的情況.
,與拋物線方程聯立,利用韋達定理以及二次函數性質求最值,此種設法已包含直線斜率不存在的情況.
解:(1)方法一:設![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
![]() ,化簡得
,化簡得![]() ,
,
因為![]() 的中點為
的中點為![]() ,
,![]() ,
,
![]() ,∴l的方程為
,∴l的方程為![]() ,即
,即![]() .
.
經檢驗,符合題意.
方法二:設![]() ,
,![]() ,
,
當斜率不存在時,顯然不成立.
當斜率存在時,設直線l:![]() ,顯然
,顯然![]() ,
,
由 得
得![]()
易知![]() ,
,![]() ,
,
因為![]() 的中點為
的中點為![]() ,
,![]() ,即
,即![]() ,
,
解得![]() ,∴l的方程為
,∴l的方程為![]()
(2)方法一:由拋物線的定義可知![]()
當斜率不存在時,直線l:![]() ,
,![]()
當斜率存在時,設直線l:![]() ,顯然
,顯然![]() ,
,
由 得
得![]() ,
,
易知![]() ,
,
 ,
,
![]() 時,
時,![]() 的最小值為
的最小值為![]()
綜上,![]() 的最小值為
的最小值為![]()
方法二:由拋物線的定義可知![]()
顯然直線l不平行于x軸,設直線l:![]() ,
,
由 得
得![]() ,
,
易知![]() ,
,![]() ,
,![]() ,
,
![]()

![]() 時,
時,![]() 的最小值為
的最小值為![]()


科目:高中數學 來源: 題型:
【題目】(1)經統計,在某儲蓄所一個營業窗口排隊等候的人數及相應概率如下:
排隊人數 | 0 | 1 | 2 | 3 | 4 | 5人及5人以上 |
概率 |
|
|
|
|
|
|
求至少3人排隊等候的概率是多少?
(2)在區間![]() 上隨機取兩個數m,n,求關于x的一元二次方程
上隨機取兩個數m,n,求關于x的一元二次方程![]() 有實根的概率.
有實根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“微信運動”是騰訊開發的一個記錄跑步或行走情況(步數里程)的公眾號用戶通過該公眾號可查看自己某時間段的運動情況.某人根據2018年1月至2018年11月期間每月離步的里程(單位:十公里)的數據繪制了下面的折線圖.根據該折線圖,下列結論正確的是( )

A.月跑步里程逐月增加
B.月跑步里程最大值出現在10月
C.月跑步里程的中位數為5月份對應的里程數
D.1月至5月的月跑步里程相對于6月至11月波動性更小,變化比較平穩
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】土筍凍是閩南種廣受歡迎的特色傳統風味小吃某小區超市銷售一款土筍凍,進價為每個15元,售價為每個20元.銷售的方案是當天進貨,當天銷售,未售出的全部由廠家以每個10元的價格回購處理.根據該小區以往的銷售情況,得到如圖所示的頻率分布直方圖:

(1)估算該小區土筍凍日需求量的平均數![]() (同一組中的數據用該組區間的中點值代表);
(同一組中的數據用該組區間的中點值代表);
(2)已知該超市某天購進了150個土筍凍,假設當天的需求量為![]() 個
個![]() 銷售利潤為
銷售利潤為![]() 元.
元.
(i)求關于![]() 的函數關系式;
的函數關系式;
(ii)結合上述頻率分布直方圖,以額率估計概率的思想,估計當天利潤![]() 不小于650元的概率.
不小于650元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某次數學測驗共有10道選擇題,每道題共有四個選項,且其中只有一個選項是正確的,評分標準規定:每選對1道題得5分,不選或選錯得0分,某考試每道都選并能確定其中有6道題能選對,其余4道題無法確定正確選項,但這4道題中有2道能排除兩個錯誤選項,另2題只能排除一個錯誤選項,于是該生做這4道題時每道題都從不能排除的選項中隨機挑選一個選項做答,且各題做答互不影響.
(Ⅰ)求該考生本次測驗選擇題得50分的概率;
(Ⅱ)求該考生本次測驗選擇題所得分數的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是菱形,點
是菱形,點![]() 在線段PC上,且三棱錐
在線段PC上,且三棱錐![]() 的體積是四棱錐
的體積是四棱錐![]() 的體積的
的體積的![]() ,
,![]() ,
,![]() 平面
平面![]() .
.
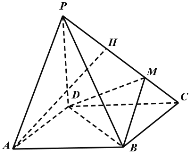
(1)若![]() 是
是![]() 的中點,證明:直線
的中點,證明:直線![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com